惑星のまわりをまわっている天体を「衛星」といいますが、その中でも人工衛星とは、私たち人間が色々な目的を成し遂げるために打ち上げた、人工的に作った衛星のことです。
今のところ人類が住んでいるのは地球のみですので、実質「地球のまわりをまわっている人工的な衛星」ということになります。
今回は、万有引力の基本問題にもあたる、人工衛星の速度を求めてみましょう。
-----------------------------
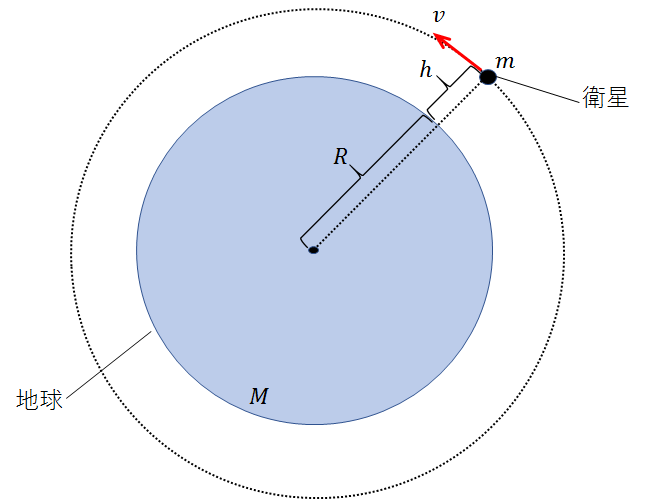
図のように、大きさの無視できる人工衛星(以下「衛星」といいます)が速度\(v\)で地球のまわりをまわっているとし、地表からの距離\(h\)は変化しないものとします。
また、地球の半径を\(R\)、地球と衛星の質量をそれぞれ\(M\)、\(m\)とします。
基本は「運動方程式」
衛星は運動していますので、出発点となるのは運動方程式\(ma\)=\(F\)です。
まずはこの運動方程式に、それぞれの量を入れてみましょう。
●質量\(m\)
そのまま衛星の質量\(m\)を入れます。
●加速度\(a\)
一般的に円運動する物体には、円の中心向きに加速度がはたらいており、その大きさは円の半径を\(r\)、物体の速度を\(v\)とすると、\(\Large\frac{v^2}{r}\)と表されます。
今回、図からもわかるように、衛星は半径\(R+h\)の円運動をしていることになるので、これを用いると加速度の大きさは\(\Large\frac{v^2}{R+h}\)となります。
●力\(F\)
衛星が地球のまわりをまわっていられるのは、地球からの引力のおかげです。
意外に思うかもしれませんが、衛星は運動方向へ自ら進んでいるわけではありません。
衛星を加速させるエンジンなどは付いていますが、これは衛星の軌道修正に使われる程度のもので、絶えず動いているわけではありません。
この引力とは、地球と衛星の間にはたらく「万有引力」のことです。
よって、衛星にはたらく力は、万有引力の式\(F\)=\(G\Large\frac{mM}{r^2}\)より、\(G\Large\frac{mM}{(R+h)^2}\)となります。
※衛星にはたらいている力が「引力のみ」というのは、衛星の運動の様子を離れた場所から見ている場合です。
今回は離れた場所から見ているとして考えています。
これが仮に衛星に乗った状態で見ると、引力の他に遠心力もはたらきます。
(向心力と遠心力の違いで、詳しく紹介しています。)
以上より衛星の運動方程式は、
\(m\Large\frac{v^2}{R+h}\)=\(G\Large\frac{mM}{(R+h)^2}\)・・・・・①
と立てることができます。
①を\(v\)について解くと、
\(v^2\)=\(\Large\frac{R+h}{m}\)・\(G\Large\frac{mM}{(R+h)^2}\)
=\(\Large\frac{GM}{R+h}\)・・・・・②
ここで\(mg\)=\(G\Large\frac{Mm}{R^2}\)・・・・・③
の関係式を使うと\(gR^2\)=\(GM\)なので、
これを②に代入すると、
\(v^2\)=\(\Large\frac{gR^2}{R+h}\)
よって衛星の速度は
\(v\)=\(\sqrt{\Large\frac{gR^2}{R+h}}\)・・・・・④
となります。
(※③の関係式は、地表の物体にはたらく万有引力と重力は等しいと見なしたものです。
なぜなら地上の物体にはたらく遠心力や微々たる高さの変化は、万有引力や地球の半径に比べると無視できるレベルだからです。)
人工衛星の速度は高度で決まる
式④において\(g\)と\(R\)は定数なので、衛星の速度は、地表からの距離\(h\)に依存していることがわかります。
高い位置では速度が小さくなり、逆に低い位置では大きくなるのです。
地球に近いと引力も大きくなり、その分加速度も大きくなるためと考えられています。