手のひらにおさまるサイズのボールを、水平に投げる状況を考えてみましょう。
今、ある人が軽く投げて、ボールが2[m]先の地面に落下したとします。

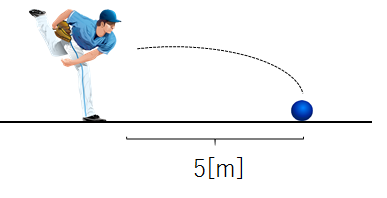
少し力を入れて投げたら、5[m]先の地面に落下しました。
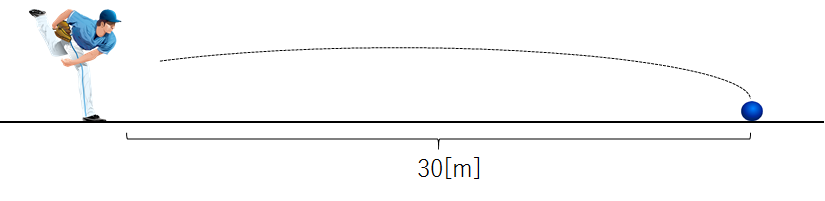
おもいきり力を入れて投げたら、30[m]先の地面に落下しました。
ボールに力を加えるということは、すなわち初速度を与えるということです。
初速度が大きくなると、その分ボールの飛距離が伸びることがわかります。
では、この初速度をどんどん大きくしていったらどうなるでしょうか?
当然飛距離も、100[m]、10[km]、100[km]、1000[km]、・・・・・と、どんどん伸びていきます。
ここで、飛距離がついに地球1周分の距離になったとし、この時の初速度を\(v_m\)としましょう。
仮に空気抵抗が無い場合、ボールは減速しませんから、初速度\(v_m\)のままずっと進み続けます。
つまり、地球のまわりをずっとまわり続けるということです。
これはまさに、地球のまわりをまわる「衛星」の動きそのものです。
-----------------------------
第1宇宙速度とは、「地球において、その高度を海抜ゼロ(海面もしくは地表すれすれ)とした(仮想上の)円軌道の衛星軌道の軌道速度(引用:wikipedia)」です。
つまり「ある物体を衛星のように、地球をまわる軌道上に乗せるための最低速度」ということです。
とにかく軌道に乗せるための速度なので、地面すれすれの高さをまわると考えます。
軌道に乗せるために与える速度の中でも、一番小さくて済みますからね。
冒頭の例だと、まさに速度\(v_m\)に該当します。
-----------------------------
この第1宇宙速度ですが、具体的な値はおよそ7.9[km/s]、時速になおすとおよそ28,400[km/h]です。
赤道上を1周がおよそ40,000[km]なので、約一時間半で地球をひとまわりしてしまうのです。
第1宇宙速度を求めてみよう
では、上記の「7.9[km/s]」というのはどのようにして出てきたのでしょうか?
「人工衛星の速度を求めてみよう」では、地表から高さ\(h\)の地点をぐるぐるまわる衛星の速度を求めました。
求め方はこれと同じで、今回は地表からの高さ\(h\)がゼロになっただけです。
地球の半径を\(R\)とすると、高さ\(h\)の地点をまわる場合、衛星は半径R+hの円運動をしていましたが、今回、高さ\(h\)はありませんので、衛星は「半径Rの円運動」をすることになります。
よって、高さhの円運動の場合にならって運動方程式を立てると、
\(m\Large\frac{v^2}{R}\)=\(G\Large\frac{mM}{R^2}\)
これを\(v\)について解くと、
\(v\)=\(\sqrt{\Large\frac{GM}{R}}\)
\(GM=gR^2\)の関係式より、
\(v\)=\(\sqrt{\Large\frac{gR^2}{R}}\)=\(\sqrt{gR}\)・・・・・①
となります。
重力加速度:\(g=9.8\)[m/s]、地球の質量:\(R=6.4×10^6\)を①に代入すると、
\(v\)=\(\sqrt{gR}\)
=\(\sqrt{9.8×6.4×10^6}\)
=\(\sqrt{98×10^{-1}×64×10^{-1}×10^6}\)
=\(\sqrt{2×49×64×10^4}\)
=\(\sqrt{2×7^2×8^2×10^4}\)
=\(7×8×10^2×\sqrt{2}\)
≒\(56×10^2×1.41\)≒\(7.9×10^3\)[m/s]
=\(7.9\)[km/s]
と求めることができます。
(第1宇宙速度よりもさらに速い、第2宇宙速度というものもあります。)