万有引力とはニュートン力学における考え方の一つで、すべての物体(質点)は、地上だけでなく宇宙全体においても互いに引き合っているというものです。
リンゴが木から落ちる様子を見たニュートンが、「惑星同士も、このリンゴと地面のように互いに引き合っているのではないか」と考えたことが始まりです。
教科書などにもありますが、二つの物体の質量をそれぞれ\(m\)、\(M\)、物体間の距離を\(r\)、万有引力定数を\(G\)とすると、万有引力\(F\)は、
\(F\)=\(G\Large\frac{mM}{r^2}\)
と表されます。

重力とは等しい?等しくない?
ここでひとつ、万有引力と重力の関係性をお話します。
万有引力が関係したいくつもの問題では、しばしば下記のような関係式が使われています。
\(mg\)=\(G\Large\frac{mM}{R^2}\)
(\(mg\):質量\(m\)の物体にはたらく重力、\(R\):地球の半径)
「地表付近の物体にはたらく万有引力は、この物体にはたらく重力に等しい」というものです。
この式を変形して代入すると、地球の質量や周回する物体の速度などを求めることができるので確かに便利なのですが、悲しいかな、
「万有引力と重力は同じものなんだな」
という誤解を招く原因となっています。
少しだけ、次にお話することを覚えておいてください。
地表にはたらく「遠心力」
既に知っているかと思いますが、太陽のまわりをまわっている地球は、自分自身も回転しています(自転)。
つまり地上にいる私たちは、円運動している地球に乗っているようなものです。
向心力と遠心力の違いでもお話しましたが、円運動している物体に観測者が乗っている時、観測者は遠心力を受けていることになりますので、私たちも地球の自転による遠心力を受けています。
また、万有引力は地球の中心方向にはたらくので、地上にいる人や物体にはたらく力を図示すると、下記のようになります。
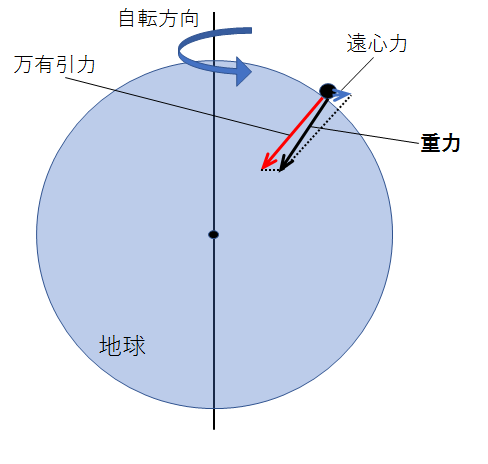
重力は万有引力と遠心力の合力で、向きは地球の中心方向ではありません。
つまりこの図から、万有引力=重力ではないことがわかります。
理由は大きさが桁違いだから
ではなぜ、問題集などでは「万有引力=重力」とした関係式が使えるのでしょうか。
その理由は、それぞれの力の「大きさ」にあります。
地球はとてつもなく大きいので、他の物体に及ぼす万有引力もとても大きくなります。
ですが地球の万有引力と比較すると、地上の物体にはたらく遠心力は、実は微々たるものなのです。
(仮に遠心力の大きさを1とすると、万有引力の大きさは何と250~300にもなります。)
要するに、万有引力と比べて遠心力はとても小さいので、無視して考えることができるのです。
例え物体が地上にあろうとも、「万有引力=重力」とみなして解いていくことができるのは、このように大きさが違い過ぎるからなのです。
なので特に断りがない限りは、問題を解く際に\(mg\)=\(G\Large\frac{mM}{R^2}\)の関係式は使って構いません。
※\(R\)は地球の半径であることに注意してください。
---------------------------
余談ですが、冒頭の万有引力の式の\(r\)は、物体の高さが地表から私たちの身長あたりまで変わったとしても、\(r\)のままで式を立てます。
なぜなら地球の半径と比べると、身長の高さ程度の変化なんてほとんど動いてないようなもので、計算上何ら影響はないからです。
例えばバランスボールの上にゴマ粒がのっていたとして、そのゴマ粒がミリ単位で動いても、バランスボールの中心とゴマ粒との距離は変わってないも同然ですよね。
このように宇宙や地球が絡む運動は、とても小さい量は無いものと見なす処理(=近似)がしばしば使われますので、頭の隅に入れておいてもらえればと思います。