力のモーメントとは物体を回転させる力のことで、他にもトルク、回転力など様々な呼び方があります。
回転に関係した力なので、剛体の力のつり合いを考える際に、よく使われます。
力のモーメントの式
ある一点Oを回転軸として、自由に回転できる棒があります。

この棒に加える力を\(F\)、点Oから力の作用点までの距離を\(r\)、棒の延長線と力の向きが成す角を\(θ\)とすると、点Oのまわりの力のモーメント\(M\)は、
\(M\)=\(Fsinθ・r\)
で求めることができます。
\(sinθ\)が付いている理由は、加える力の、棒に対して垂直な成分を出すためです。
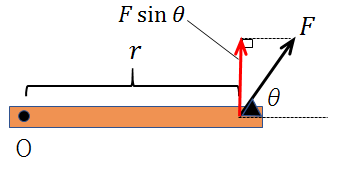
なぜならば力のモーメントを考える時、加える力の向きは、回転軸から作用点までの向きに対して垂直でなければならないという、大切な決まりがあるからです。
(この例では、たまたま「(回転軸から作用点までの向き)=(棒の向き)」なので、力の向きが棒に対して垂直であれば決まりを満たします。)
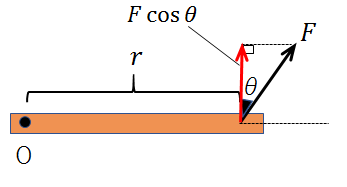
なお、\(θ\)の取り方によっては、垂直な成分が\(Fcosθ\)となるので注意してください。
力のモーメントの具体例
静止している剛体にいくつかの力がはたらいているとき、その力のモーメントの総和がゼロであれば、剛体にはたらく力はつり合っていると言えました。
これに関する、シンプルな例を以下に示します。
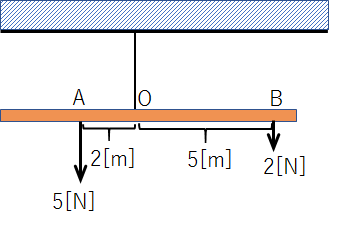
上図において、棒は水平に静止しているとします。
各点にかかる力の向きが棒に対して垂直であるとすると、
点Aにかかる力について、点Oのまわりの力のモーメントは、5[N]×2[m]
点Bにかかる力について、点Oのまわりの力のモーメントは、2[N]×5[m]
なお、点Oを回転軸とした時、回転させようとする力の向きは、点Aと点Bで互いに逆となっています。
よって、仮に反時計回りを正とすると、時計回りに回転させようとする点Bにはたらく力は、負になります。
よって、力のモーメントの総和は、
5[N]×2[m]-2[N]×5[m]=0
力のモーメントの総和がゼロなので、この剛体にはたらく力はつり合っていると言えます。
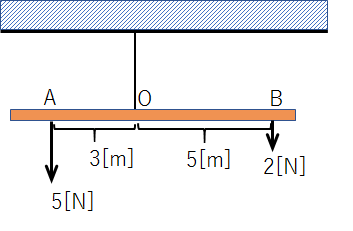
もしも、点Aが1[m]だけ左よりの場合だと、
点Oのまわりの力のモーメントが5[N]×3[m]となるので、総和がゼロになりません。
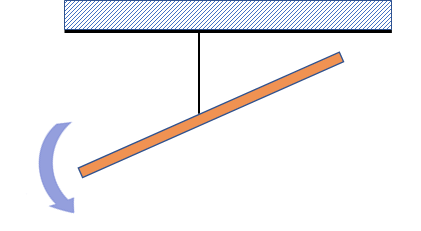
この場合、棒は半時計回りに回転してしまいます。
---------------------------------
今度は試しに、点Bを回転軸としてみましょう。
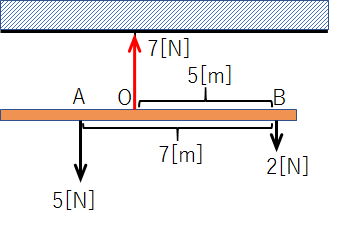
鉛直方向の力のつり合いより、糸の張力(上向きの力)は7[N]であることを踏まえると、
点Aにかかる力について、点Bのまわりの力のモーメントは、5[N]×7[m]
点Oにかかる力について、点Bのまわりの力のモーメントは、7[N]×5[m]
この場合も、点Aと点Oにかかる力は互いに逆向きなので、
力のモーメントの総和は、5[N]×7[m]-7[N]×5[m]=0となり、つり合っていることがわかります。
このように基準となる回転軸は、点O以外にも定めることができるのです。
なお、回転軸自体にはたらく力は、力のモーメントのつり合い式に含まなくてもよいことを覚えておいてください(この場合、点Bにはたらく2[N]のこと)。