ここでは一つの物体ではなく、「物体をのせた物体」の運動の具体例を挙げて、ポイントを説明していきたいと思います。
動き方は二通りある
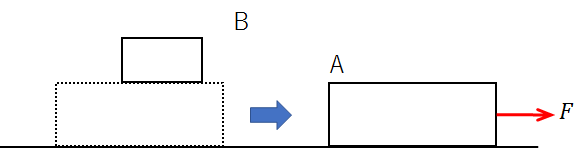
図のように、水平でなめらかな床の上に質量\(M\)の物体Aが置かれています。
物体Aの上には、さらに質量\(m\)の物体Bがのっており、物体AとBの間には摩擦があるものとします。

この状態で、物体Aに右向きの力を加えると、二つの物体はどのように動くでしょうか?
結論から言ってしまえば、条件によって動き方は二通りあります。
●物体AとBが一体となって動く
●物体AとBが別々に動く
なぜこのような違いが出てくるのか・・・。
カギを握るのは、物体Aに加える力の大きさと摩擦力です。
まずは、一体となって動くパターンから見ていきましょう。
摩擦があるから一体となる
物体AとBにはたらく力をそれぞれ図示すると、下記のようになります。
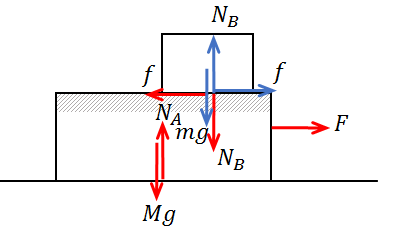
(物体A)
\(F\)・・・物体Aに加える力
\(Mg\)・・・物体Aにはたらく重力
\(N_A\)・・・物体Aが床から受ける垂直抗力
\(f\)・・・物体Aにはたらく摩擦力
\(N_B\)・・・「物体Bが物体Aから受ける垂直抗力」の反作用
(物体B)
\(mg\)・・・物体Bにはたらく重力
\(N_B\)・・・物体Bが物体Aから受ける垂直抗力
\(f\)・・・物体Bにはたらく摩擦力
一緒に書くと非常に分かり辛いので(笑)、物体ごとに分けてみました。

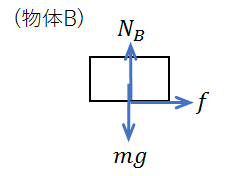
力を図示する際に忘れやすいのが、物体Aにはたらいている\(N_B\)という力です。
物体Bが上にのっているので、物体Bが受ける垂直抗力と同じ力を受けています。
(当然、物体Aが置いてある床も、「物体Aが床から受ける垂直抗力」の反作用の力を受けています。今回は物体Aと物体Bにはたらく力のみを考えているので、図示していないだけです。)
また、物体AとBは接しているので、摩擦力\(f\)は同じ大きさで、互いに逆向きです。
-----------------------------
さて、ここで水平向きにはたらいている力を見てみますと、\(F\)以外では、摩擦力\(f\)だけです。
つまり、二つの物体が一体となって進む理由は単純で、摩擦があるからなのです。
もしも二つの物体の間に摩擦が無いと、物体Aだけが右向きに移動し、物体Bはそのまま同じ場所に居座った状態となります。
ちなみに、一体となって進むということは、言いかえれば、物体Aから見て物体Bは静止しているということです。
よって、この時の摩擦力\(f\)は静止摩擦力となります。
静止摩擦力の限界は?
静止摩擦力がはたらいているおかげで、力\(F\)を加えても物体Bは動き出さず、結果的に一体となって進むわけですが、静止摩擦力にも持ちこたえられる限界があります。
ここで、加える力\(F\)を大きくしていき、今まさに物体Bが動き出す瞬間の状態であるとしましょう。
この時、静止摩擦力は限界ギリギリの状態です。
この状態の静止摩擦力を「最大静止摩擦力」といい、静止摩擦係数と垂直抗力の積で表されます。
この状態から物体Aに加える力が少しでも大きくなると、ついに静止摩擦力が持ちこたえられなくなり、物体Bは物体Aの上を動いてしまいます。
動いている時も摩擦力がはたらく
物体Aに加える力が最大静止摩擦力を超えると、物体Bは物体Aの上を動きます。
ここでポイントとなるのが、物体Bが動く向きです。
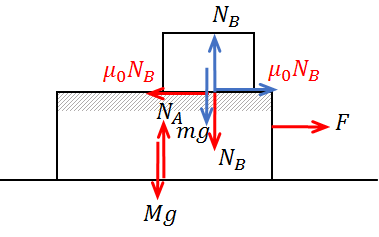
まず、この状態における物体AとBにはたらく力をそれぞれ図示すると、次のようになります。
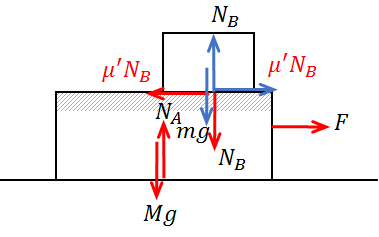
二つの物体にはたらく摩擦力を\(μ'N_B\)と書きました。
これは、動いている物体にはたらく摩擦力で、動摩擦力といいます。
物体Bに着目すると、水平向きにはたらいている力はこの動摩擦力のみです。
したがって、物体Bは水平方向右向きに移動します。
理由は簡単で、物体Bにはこの右向きの力しかはたらいていないからです。
物体は必ず、はたらいている力の向きに運動します。
複数の力がはたらいている時は、大きい方の力の向きに移動します。
如何にはたらく力を描けるか
物体の上に物体がのった状態では、各物体にはたらく力を正確に書き出すことが大切になってきます。
特に二つの物体が接している場合、相手に力を及ぼせば、必ず自分も同じ力を受けることを覚えておいてください。
(摩擦力\(f\)、\(μ'N_B\)、垂直抗力\(N_B\)など)
なお、物体Bが動くケースについては演習問題もありますので、参考にしてみてください。