速さと速度の違い

速さと速度は、どちらも物理現象を紐解くためにとても重要で、問題としてもよく出てきます。

ここで今一度、両者の違いについておさらいしておきましょう。

運動には必ず向きがある

初めに、速さと速度がもっている性質を、簡単に書いてみます。

上記からわかるように、速さと速度の違いはズバリ、「向きを持っているか持っていないか」です。

中学校までの理科では、速さしか習いませんでした。

それは、運動している向きまで深く考えることが無かったからです。

果たして、この「向き」というのは具体的にどのようなものでしょうか。

例として、まずは次のような問題を考えてみます。

速さについては、小学校で習った「速さ＝距離／時間」という公式に当てはめると、すぐ出てくるかと思います。

６００[m]／３０[s]＝２０[m/s]ですね。

問題は、この車の「速度」です。

初めに書いたとおり、速度も速さと同じく大きさを持っており、それは、速さと同じ２０[m/s]です。

ですが、大きさに加えて向きを持っている「速度」は、少なくともこの問題では求められません。

なぜならば、車が進んでいる方向が、問題文に与えられていないからです。

--------------------

では、上記の問題を少し変えた、次のような問題を考えてみます。

先程の問題文と違う点に気がついたでしょうか？

「西向き」という、車の進む向きが決められていますよね。

また、「東向きを正とする」といった条件も与えられています。

ここで初めて、速度を求めることができます。

まず速さは、前の問題と同様に６００[m]／３０[s]＝２０[m/s]。

これは速度の大きさでもあることは、お話したとおりです。

そして車の速度ですが、今回車は、東とは真反対の西向きに進んでいますので、２０[m/s]にマイナスをつけた、－２０[m/s]が正解です。

図で表すと、次のようになります。

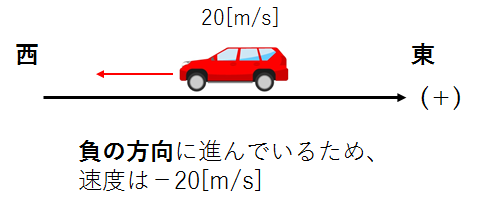
このように、速度を求めたい場合は、物体の運動している「向き」を考慮しなければなりません。

関係が深い「物理」と「ベクトル」

速度のように「大きさ」と「向き」を持ったものとして、他にも高校数学で習う「ベクトル」があります。

そもそもなぜ、高校物理では速さと速度を区別しなければならないかといいますと、この「ベクトル」を使って、物体の運動の向きを考えるようになるからです。

今回お話した速度以外にも、物体にかかる力や運動方向を記述する際に、ベクトルはとてもよく使うことを、頭に入れておいてください。

（おそらく中学までの理科で速度を習わなかったのは、ベクトルを習わないことも関係しているのではないかと思います。）

まとめ