今回は、流れている川の上を渡る問題を扱っていきます。
特に相対速度の項目で目にすることが多いので、少しずつ頭に入れておいてくださいね。
頻出のシチュエーション
既に問題集などで見たことがあるかと思いますが、問題としてよく出てくるのが、流れている川の上を、船を使って反対側の岸へ渡るケースです。
この時、問題文中に条件として与えられることが多いのは、下記のようなものです。
●川の流れの速さ
●静水中を進む船の速さ
●川幅
「静水中」というのは聞き慣れない言葉かもしれませんが、「流れが無い水の上」のことです。
例えば、静かな森の中の湖をイメージしてもらえればと思います。
問題に登場する「川」は流れがあるため、静水とは言えません。
海も波の勢いがあるので、静水ではないですね。
つまりこのような問題は、静かな水の上でこれだけ進める船が、流れがある川を横切るとどれだけ影響を受けるのよ!というのを解き明かしていく問題なのです。
-----------------------
向かって左側を上流とした場合、川を船で横切っていくと、流れの勢いで船の進む方向が影響を受けてしまいます。
例え、船の先端を対岸に真っすぐ向けていてもです。
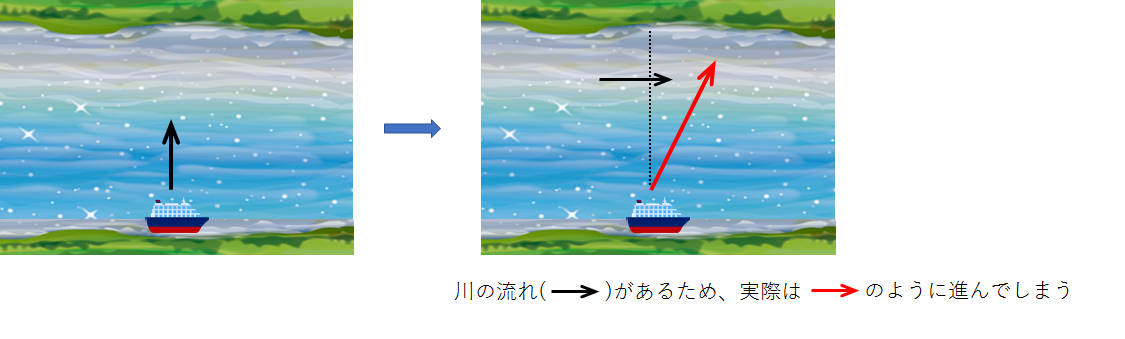
船は、一生懸命真っすぐ進もうとしているわけですが、川の流れにおされて、「結果的に」斜めに進んでしまうことになります(少なくとも高校物理では、意識的に流れに逆らって蛇行するような動きは考えません)。
ですので、「結果的に」真っすぐ進むためには、初めから真っすぐの方向でスタートせず、あらかじめ船を上流に向けてスタートする必要があるのです。
この時によく問われるものとして、
●真っすぐ進むためには、川岸に垂直な方向から、どのくらい船を上流に向けてスタートすればよいか
●対岸に到達するまでにかかる時間はどのくらいか
などがあります。
また、「平面上の相対速度」でも紹介しましたが、今回の船の問題も、解いていくうえでベクトルを使うことが多くなっています。

川を横切る問題の具体例
では、ここで実際に例題を見ていきます。
(例題)
静水中を8.0[m/s]で進む船が、4.0[m/s]の速さで流れる幅20[m]の川を横切るため、船首を川岸に対して直角に向けてスタートした。
(1)対岸に到達するまでの時間を求めよ
(2)船は、出発地点の真向かいの対岸地点から、何m下流の地点に到達するか
(3)真っすぐ対岸に到達するためには、船を対岸から何度上流に向けてスタートすればよいか
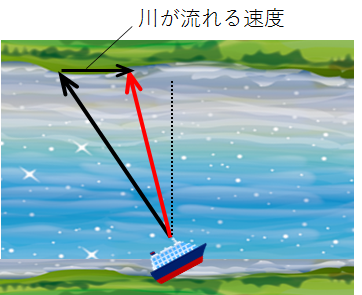
与えられた条件を黒ベクトルで、実際の船の経路を赤ベクトルでそれぞれ図示すると、下記のようになります。
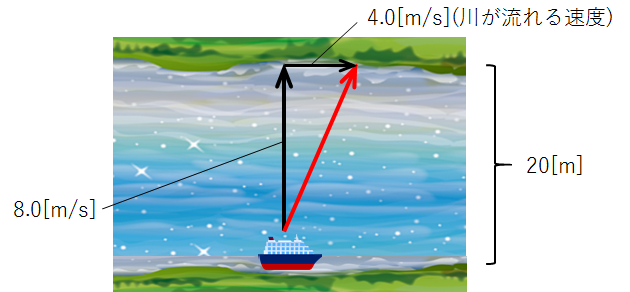
-----------------------
まず(1)について、
時間は、「距離/速さ」で求めることができるので、問題文からそれぞれの数値を探し出します。
距離については、川幅の20[m]が与えられていますね。
ちなみに実際の船の速度の大きさ(=速さ)ですが、上記の図から三平方の定理を用いて、
$$\sqrt{(8.0)^2+(4.0)^2}=4\sqrt{5}$$
と導き出せます。
ですが、川幅をこの値で割ってはいけません。
ここは、非常に間違えやすい点です。
なぜなら、斜めに進んだことで、実際の船の移動距離は20[m]よりも長くなっているからです。
では、川幅を割ることができるのは何かといいますと、川の流れに垂直なもの、つまり船の速度の鉛直成分です。
実際に進んだ船の経路は確かに斜めの方向ですが、これはそもそも、「真っすぐ進もうとする船の速度」と「川の流れる水平向きの速度」を合成したものです。
ですので、斜めの速度は鉛直成分と水平成分に分解して考えることもでき、鉛直成分であれば真っすぐに川幅だけ進んでいますから、川幅を割ればかかった時間が求められます。
つまり、対岸に到達するまでの時間は、
20[m]/8.0[m/s]=2.5[s]
となります。
-----------------------
(2)については、本来なら船は真向かいの対岸地点に到達するつもりが、川の流れのせいで少し下流に到達したということです。
ここで使えるのは、水平向きの速度、すなわち川の流れる速度です。
船が対岸に到達するまでの時間は(1)より2.5[s]でしたから、船はスタートしてから2.5[s]までの間、ずっと川の流れに影響されていたことになります。
ですので求める距離は、
4.0[m/s]*2.5[s]=10.0[m]
船は、「真向かいの対岸地点から10.0[m]下流の地点に到達した」ことになります。
-----------------------
最後に(3)ですが、これは結果的に真っすぐ進むために、船をあらかじめ上流に向けてスタートしています。
船は、あくまで最初に向けた方向に、静水中の速さ(8.0[m/s])で一生懸命進もうとします。
図に表すと、下記のような状況ですね。
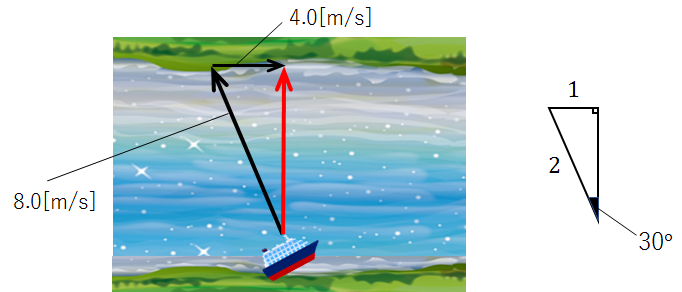
そして「結果的に」真っすぐ進んで対岸に到達できた、というわけです。
川が流れる速度は一定ですから、求める角度は三角比の公式より、「30度」となります。
船の速度の鉛直成分は不変
あらためて例題を見てみますと、船が少し下流にずれて到達したのは、当然、川の流れの影響を受けたからです。
つまり、変化するのは船の速度の水平成分で、鉛直成分は、その方向に影響を与えるものが無いので何ら変化しないことが分かります。
これは結果的に真っ直ぐ進まなくても、例えば下記のような経路をたどっても同じことです。
途中で船が加速したり、鉛直方向に何か力を受ければ速度の鉛直成分も変化しますが、今回の例のように普通に川を渡る場合は、速度の鉛直成分は変化しないと考えておいてください。
そして、
●船は静水中の速さで一生懸命進もうとしている
●しかし、川の流れの影響を受けて「結果的に」経路が変化した。
このようなイメージを持ってもらえればと思います。