平面上を運動する物体の相対速度

相対速度では、一直線上を運動する物体の相対速度について考えました。

今回は、物体の運動の範囲を少し広げて、平面上を運動する場合の相対速度についてお話していきたいと思います。

考え方は一直線上の場合と同様ですので、少しずつ見ていきましょう。

相対速度の求め方

まず初めに、相対速度の求め方についてのおさらいです。

「○○に対する相対速度」というのは、見ている側を基準とした速度のことで、「運動を見られる側」の速度(\(v_B\))から、「運動を見ている側（基準）」の速度(\(v_A\))を引いたものです。

この相対速度、平面上の運動の場合はどのように求めれば良いでしょうか？

具体的に例題を取り上げてみます。

「物体Aに対する」とありますので、物体Aから見た物体Bの相対速度を求めます。

つまり、「物体Aから見ると、物体Bはどのように見えるんだろう？」ということです。

先程と同じように、物体Bから物体Aの速度を引けば求められますが、それぞれの運動方向が一直線上に無いため、単純に引き算ができません。

このような場合は、数学で習う「ベクトル」を使います。

平面上の相対速度はベクトルの引き算

ベクトルとは、大きさと向きを持った量で、下記のように矢印で表します。

上記のような例題を解く上で欠かせないものが、「ベクトル同士の引き算」です。
例えばベクトル\(\vec{a}\)からベクトル\(\vec{b}\)を引いた結果(\(\vec{a}-\vec{b}\))は、下図の赤線になります。

慣れないうちは混乱しがちですが、「引くほうのベクトルの先端から、引かれるほうのベクトルの先端に向かう矢印」です。

ここで例題に戻って、物体A、Bの運動の様子を大まかにベクトルで表すと、次のようになります。

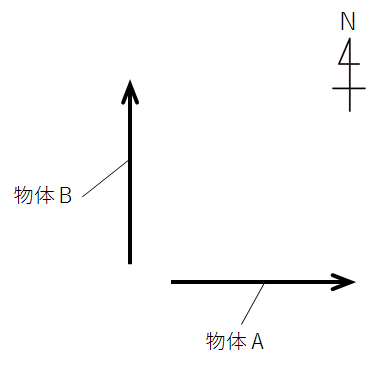
先程のベクトルの引き算の要領で引いた結果が、こちらです。

この結果から、物体Aから見た物体Bの運動方向が分かります。

次に相対速度の大きさですが、今回物体AとBの速度の大きさは等しいため、三角比から、次のように求められます。

つまり、物体Aに対する物体Bの相対速度は、北西向きにおよそ84.84[km/h]です。

-----------------------

今回は相対速度を求めるためにベクトルを使いましたが、ベクトルは、物理の問題を解く上で欠かせない「武器」です。

高校物理では、物体も縦横様々な方向に運動するため、相対速度以外にもベクトルを使って解く機会がたくさんあることを、意識しておいてください。