単振動をしている物体の動きは、同じ物体が等速円運動している状況を「真横」から見た状態に相当します。
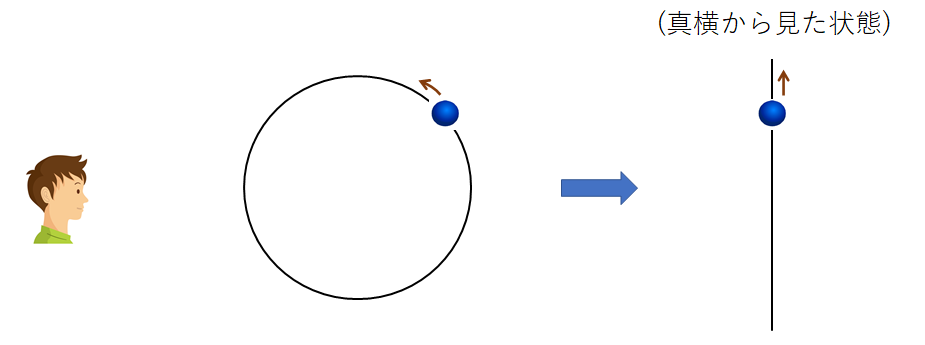
このような場合、物体は「上下運動」をしていますね。
そして、円運動の振幅を\(A\)、角速度を\(ω\)、時間を\(t\)とすると、単振動する物体の変位\(x\)、速度\(v\)、加速度\(a\)は、それぞれ下記の式で表されます。
・\(v=Aωcosωt\)
・\(a=-Aω^2sinωt=-ω^2x\)
これらの式は色々な参考書等で取り上げられているので、見たことある人も多いかと思います。
もちろんこの式を丸暗記していれば問題は解けますが、なぜ加速度の式だけマイナスがついているのでしょうか?
単振動に関する重要な性質が絡んでいるので、少し説明したいと思います。
------------------------------------
あらためて、単振動する物体の加速度の式を見てみましょう。
この式から、加速度は変位に依存していることがわかります。
つまり、変位が大きくなると加速度も大きくなり、逆に変位が小さくなると加速度も小さくなります。
そしてマイナスの符号は、加速度が移動方向と逆向きに生じることを意味しています。
例えばある物体が原点を中心に水平に単振動している場合、物体が右向きに移動している時は左向き、逆に左向きに運動している時は右向きに加速度が生じているということです。
さらに運動している物体には、運動方程式が使えるのでした。
物体の質量を\(m\)[kg]、物体にはたらいている力を\(F\)[N]、加速度を\(a\)[m/s]とすると、この物体の運動方程式は、
\(F=ma=m(-ω^2x)=-mω^2x\)
これより、物体にはたらいている力も、加速度と同じく移動方向と逆向きであることがわかります。
大きさは原点からの変位に比例するので、物体が端に行くほど大きくなり、原点を通過する瞬間はゼロになります。
つまり、この力は物体を常に振動の中心(ここでは原点)に戻そうとしており、これによって物体は単振動をし続けることができるのです。
------------------------------------
単振動は、振動の中心を軸に絶えず行ったり来たりしている運動なので、もしも移動方向と同じ向きに加速度がはたらいてしまうと、物体は振動の中心まで戻ってこれません。
このため、単振動が成り立つには、物体にはたらく力も、それが引き起こす加速度も、常に移動方向と逆向きにはたらかなければいけないのです。