自由落下では、ボールを持ち上げて、そっと手を離す状況を例に挙げました。
今回ご紹介する鉛直下方投射と鉛直上方投射も、自由落下と状況は似ていますが、明確な違いがひとつあります。
それは、ボールの投げ初めに初速度(勢い)を与える点です。
ボールを持ち上げるまでは自由落下と同じですが、
そっと離す
⇒自由落下
勢いよく下向きに投げつける
⇒鉛直下方投射
勢いよく上向きに放り投げる
⇒鉛直上方投射
このような違いがあります。(「鉛直」なので、それぞれ真下、真上に投げていると思ってください)
基本の式に当てはめる
鉛直下方投射も鉛直上方投射も、ベースとなるのは下記の等加速度直線運動の式です。
$$v=v_0+at$$
$$x=v_0t+\frac{1}{2}at^2$$
$$v^2-v_0^2=2ax$$
まず鉛直下方投射の場合、
自由落下と同じく、落下する物体には重力加速度が生じています。
初速度\(v_0\)については、自由落下とは異なりゼロではありません。
すなわち、式中の\(v_0\)はそのままで、aにgを当てはめて、下記のようになります。
$$v=v_0+gt$$
$$y=v_0t+\frac{1}{2}gt^2$$
$$v^2-v_0^2=2gy$$
この式は、鉛直下向きを正とした場合であることに注意してください。
------------------------
次に、鉛直上方投射を見ていきます。
鉛直上方投射の物体の動きですが、投げ上げた瞬間からしばらくの間、物体は上向きに上昇していきます。
ですが、どんどんスピードが落ちていって一瞬静止し、今度は下向きに落ちていきます。
一般的に、等加速度直線運動の式に当てはめた式としては、下記のようなものがよく見られます。
$$v=v_0-gt$$
$$y=v_0t-\frac{1}{2}gt^2$$
$$v^2-v_0^2=-2gy$$
この式は、鉛直上向きを正とした場合の式です。
今回、初速度\(v_0\)は上向きなのでプラス、重力加速度gは下向きなので、マイナスの符号が付いています。
もし仮に鉛直下向きを正とするならば、重力加速度ではなく、上向きである初速度にマイナスの符号が付きます。
ですが、どちらかと言えば初速度がプラスになる向き(=鉛直上向き)を正とした方が、問題を解くうえでは混乱しにくいかと、経験上思います。
鉛直上方投射の具体例
ここでひとつ、鉛直上方投射の例題を見ていきましょう。
(例題)
ある物体を、ビルの屋上から鉛直上向きに19.6m/sで投げ上げた。次の問いに答えよ。
ただし、重力加速度の大きさを9.8\(m/s^2\)とし、物体とヒトの大きさは考えないものとする。
(1) 物体が最高点に達する時刻\(t_1\)[s]を求めよ。
(2) 物体が達する最高点の、屋上からの高さh[m]を求めよ。
(3) 投げ上げてから10秒後に、物体は地上に到達した。ビルの高さH[m]を求めよ。
この例題の状況を図示すると、下記のようになります。
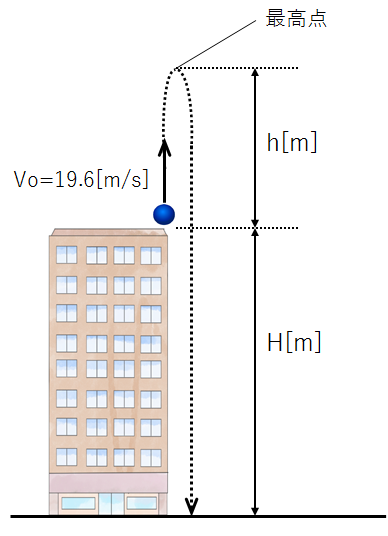
物体の動きは、投げ上げられた後しばらく上向きに進み、最高点で一瞬静止して、その後は重力にまかせて下向きに落ちていきます。
------------------------
まず(1)ですが、最高点に到達した物体の大きな特徴は、速度がゼロになることです。
逆に言えば、物体の勢いが無くなった瞬間に達していた位置、それが最高点というわけです。
今回、鉛直上向きに投げ上げているため、鉛直上向きを正として、鉛直上方投射の式を使います。
条件として与えられているのは初速度\(v_0\)と重力加速度gなので、一番目の式「\(v=v_0-gt\)」が使えそうです。
この式のvに0[m/s](速度がゼロになったので)、\(v_0\)に19.6[m/s]、gに9.8\([m/s^2]\)をあてはめると、
\(0=19.6-9.8*t_1\)
\(∴ t_1=2.0[s]\)
物体は、投げ上げてから2秒後に、最高点に達することが分かります。
------------------------
次に(2)ですが、これは投げ上げた地点から最高点までの変位ですから、鉛直上方投射の二番目の式「\(y=v_0t-\frac{1}{2}gt^2\)」にそのまま値を代入して求めることができます。
最高点に達した時刻は(1)より2秒後なので、最高点の高さh[m]は、
\(h=19.6*2-\frac{1}{2}*9.8*2^2=19.6[m]\)
となります。
------------------------
最後に(3)ですが、図を見てみると、ビルの高さというのは、物体を投げ上げた地点から地上までの長さです。
これはすなわち、物体が運動を開始した地点と、運動を終了した地点とも言えます。
ここでもう一度、鉛直上方投射の変位の式を見てみましょう。
$$y=v_0t-1/2gt^2$$
この式の「y」は、物体の「変位」を表しています。
変位とは、観測を始めてからある時刻の間までの、物体の位置の変化量のことです。
つまり、物体が最初の位置からどれだけ変化したか、というのが変位です。
物体が実際に進んだ経路の長さではありません。あくまで、スタート地点とゴール地点との差を言います。
今回、10秒後に地上に達したとありますので、\(y=v_0t-\frac{1}{2}gt^2\)に各値を代入すると、
\(19.6*10-\frac{1}{2}*9.8*10^2\)
\(=196-490\)
\(=-294[m]\)
数値にマイナスが付く理由は、投げ上げた位置を基準(=0)として、基準から上側を正、下側を負としているためです。
ビルの高さは「大きさ」なのでプラスの値ですから、答えは294[m]となります。
((3)の別解)
問題文より、投げ上げてから地上に達するまでの時間が10秒、このうち最高点に達するまでは、(1)より2秒かかっているので、
最高点から地上に到達するまでは、10-2=8秒かかっていることになります。
最高点から地面までは、物体は自由落下運動をしていますから、自由落下の変位の式\(y=\frac{1}{2}gt^2\)に各値を代入すると、
\(19.6+H=\frac{1}{2}*9.8*8^2\)
\(∴ H=294[m]\)
となります。
今回用いた自由落下の変位の式は、元々鉛直下向きを正とした時場合の式ですので、結果もそのままプラスの値となります。
※別解では、変位yに当てはめるのは(「投げ上げた地点から最高点までの高さ」+「求めたいビルの高さ」)であることに注意してください。