(問)
図のように、あらい水平面に質量Mの物体Aが置かれており、なめらかな滑車を介して質量mの物体Bと糸で水平につながれて静止している。

重力加速度をg、水平面の静止摩擦係数及び動摩擦係数をそれぞれμ、μ'として、以下の問に答えよ。
(1)物体Aがすべり出すための条件を求めよ。
(2)物体Aがすべり出した時、その加速度と糸の張力の大きさを求めよ。
問題文には「あらい水平面」とありますので、物体Aと面との間には摩擦がはたらいています。
これを踏まえて、各物体にはたらいている力を図示してみます。
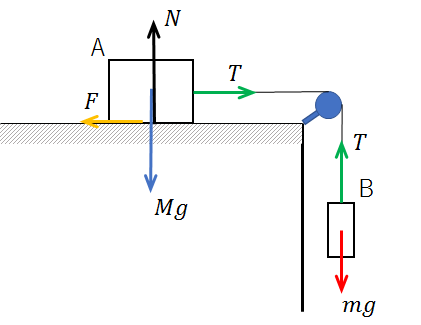
(物体A)
\(T\)・・・糸の張力
\(F\)・・・物体Aと面との摩擦力
\(Mg\)・・・物体Aにはたらく重力
\(N\)・・・垂直抗力(←物体Aにはたらく重力\(Mg\)の反作用)
(物体B)
\(mg\)・・・物体Bにはたらく重力
\(T\)・・・糸の張力
---------------------------
(1)静止している時、各物体に働く力はつり合っているので、
物体Aについては、
\(T\)=\(F\)・・・①
\(N\)=\(Mg\)・・・②
物体Bについては、
\(T\)=\(mg\)・・・③
が成り立ちます。
物体Bの質量をどんどん大きくしていった時、糸を通じて物体Aに右向きの力がはたらきますが、すべり出す直前まで摩擦力が持ちこたえるので静止しています。
この、ギリギリまで頑張っている時の摩擦力を「最大静止摩擦力」といい、静止摩擦係数と垂直抗力を用いて、下記のように表します。
最大静止摩擦力:\(Fo\)=\(μN\)
つまり、すべり出す直前において、物体Aにはたらく摩擦力は最大静止摩擦力(=\(Fo\))となります。
上記の最大静止摩擦力の式と、①~③式を使うと、すべり出す直前の物体Aにはたらく力のつり合い式は、
\(mg\)=\(μMg\)
この状態から少しでも物体Bの質量が大きくなると、摩擦力は右向きの力に負けます。
つまり、
\(mg\)>\(μMg\)
となった時、物体Aは動き出すということです。
よって求める条件は、
\(m\)>\(μM\)
となります。
---------------------------
(2)物体Aは物体Bに引っ張られてすべり出すので、移動中も糸はピンと張ったままです。
よって、糸の張力と、二つの物体の加速度は同じです。
まず行うのが、各物体について運動方程式を立てることです。
●運動方程式
ある質点の質量を\(m\)、加速度を\(a\)、かかる力を\(F\)とすると、下記の式が成り立つ。
$$ma=F$$
なお、(2)では物体Aは運動していますので、物体Aと面との間にはたらく摩擦力は「動摩擦力」となります。
動摩擦力は、動摩擦係数と垂直抗力を用いて、下記のように表します。
動摩擦力:\(F'\)=\(μ'N\)
各物体について運動方程式を立てることができれば、あとはこれらを連立方程式として解くことで求められます。
加速度を\(a\)とすると、各物体の運動方程式は、
(物体A)
\(Ma\)=\(T\)-\(μ'Mg\)・・・・・③
(物体B)
\(ma\)=\(mg\)-\(T\)・・・・・④
③と④を連立方程式として辺々を加えると、
\(Ma\)+\(ma\)=\(mg\)-\(μ'Mg\)
\((M+m)a\)=\((m-μ'M)g\)
これを解いて、
\(a\)=\(\frac{m-μ'M}{M+m}g\)・・・・・⑤
また、④より\(T\)=\(mg\)-\(ma\)であるから、これに⑤の結果を代入すると、
\(T\)=\(mg\)-\(m\frac{m-μ'M}{M+m}g\)
=\(\frac{mg(M+m)-m^2g+μ'Mmg}{M+m}\)
=\(\frac{Mmg+m^2g-m^2g+μ'Mmg}{M+m}\)
=\(\frac{(1+μ')Mmg}{M+m}\)
---------------------------
最後に、補足も兼ねてこの問題のポイントを簡単に書いておきます。
(ポイント1 ~運動方程式は各物体それぞれについて立てる~)
着目する物体を決めたら、その物体が受ける力を全て考えます。
運動方程式にもある\(F\)は、立てようとしている物体が移動中に働いている力を、全て書かなければなりません。
(ポイント2 ~物体が置かれている面の状態に注意~)
摩擦のあるなしは、直接問題文にかかれていないことが多く、代わりに面の状態が条件として与えられていることが多いです。
・なめらかな水平面→摩擦がない
・あらい水平面→摩擦がある
なお、摩擦力は必ず、物体の運動方向とは逆向きに働きます。
(ポイント3 ~力のつり合いの有無に注意~)
物体が静止していたり等速で運動している場合、その物体に働く力はつりあっています。
物体が加速度運動している場合、その物体に働く力はつりあっていません。