図のように、長さが\(l\)の糸に質量\(m\)のおもりをつけ、鉛直線と糸がなす角が\(θ\)となるように、水平面内で等速円運動をさせた。
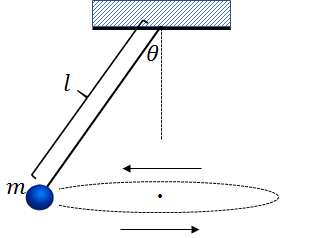
このとき、下記の二通りの方法でおもりの円運動の周期を求めよ。
なお、糸の張力を\(S\)、重力加速度を\(g\)とする。
(1)運動方程式を立てる方法
(2)力のつり合い式を立てる方法
振り子の中でも「円錐振り子」について、円運動の周期を求める問題です。
既に勘づいた人もいるかもしれませんが、「二通りの方法で求める」ということは、どちらの方法を使っても結果が同じになるということです。
ですがここは考え方が大切なので、ひとつずつ見ていきたいと思います。
運動方程式を立てる方法
運動するおもりに着目すると、はたらいている力は、重力\(mg\)と張力\(S\)です。
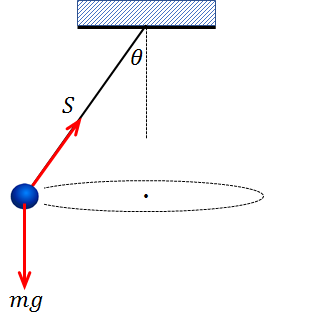
張力を水平方向と鉛直方向に分解すると、下記のようになります。
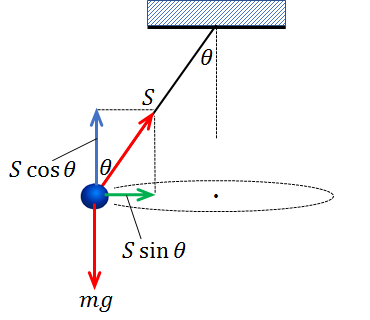
ここでとても大切なのが、張力の水平成分\(Ssinθ\)です。
向心力と遠心力の違いでもお話しましたが、物体が円運動するためには、円の中心に向かう力(=向心力)が必要です。
\(Ssinθ\)は円の中心に向かう力なので、まさに今回の円運動の向心力にあたります。
そして向心力が発生しているということは、同じ向きに加速度も発生しています(運動方程式\(F\)=\(ma\)より)。
一般的に、物体が半径\(r\)の円運動をしている時、角速度を\(ω\)とすると、生じる加速度は、\(rω^2\)と表されるので、これらを踏まえて円運動の中心方向の運動方程式を立てると、
\(mrω^2\)=\(Ssinθ\)・・・・・①
となります。
\(rω^2\)が運動方程式\(ma\)=\(F\)の\(a\)、\(Ssinθ\)が\(F\)にあたります。
これは、物体に向心力のみがはたらいているとみなす場合、すなわち、振り子の運動を見ている観測者が地上にいる場合に立てられる式です。
また、おもりには鉛直方向にも力がはたらいていますが、円錐振り子ではおもりは鉛直方向に運動しないため、これらの力はつり合っています。
よって、鉛直方向の力のつり合い式より、
\(Scos\)=\(mg\)・・・・・②
なお、今回糸の長さは\(l\)なので、円運動の半径\(r\)は\(lsinθ\)・・・・・③ と表すことができます。
②より\(S\)=\(\Large\frac{mg}{cosθ}\)であるから、これと③をを①に代入すると、
\(m(lsinθ)ω^2\)=\(\Large\frac{mgsinθ}{cosθ}\)
\(ω^2\)=\(\Large\frac{g}{lcosθ}\)
\(ω\)=\(\sqrt{\Large\frac{g}{lcosθ}}\)
よって、円運動をする物体の周期\(T\)は\(\Large\frac{2π}{ω}\)と表されるので、
\(T\)=\(\Large\frac{2π}{ω}\)=\(2π\sqrt{\Large\frac{lcosθ}{g}}\)
です。
力のつり合い式を立てる方法
運動方程式ではなく力のつり合い式から周期を求めるということは、向心力に加え、遠心力もはたらいていると仮定するということです。
ちなみに遠心力は、物体に乗って一緒に運動している観測者にはたらく力です。
運動方程式を立てて解いたパターンは、物体に向心力のみがはたらいているとしたもので、観測者が物体の運動を地上で見ているケースにあたります。
ここでは、観測者が物体と一緒に円運動しているとして、観測者に向心力と遠心力がはたらいているとみなして解いていきます。
この場合、おもりにはたらく力を図示すると下記のようになります。
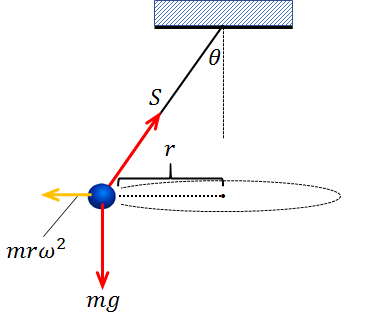
物体と一緒に円運動している観測者からは、物体にはたらくすべての力(重力と張力と遠心力)がつり合っているように見えます。
なお、物体が半径\(r\)の円運動をしている時、角速度を\(ω\)とすると、向心力は\(mrω^2\)と表されるので、遠心力の大きさも\(mrω^2\)です。
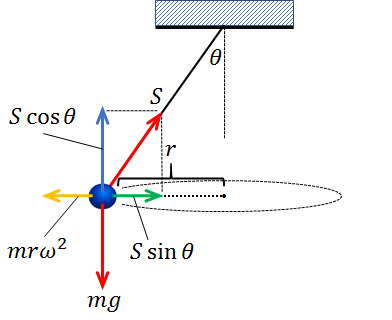
よって、張力を分解して考えると、水平方向の力のつり合い式は、
\(mrω^2\)=\(Ssinθ\)・・・・・④
となります。
これは①と同じ形です。
したがって、②と④を使えば、張力\(T\)は\(2π\sqrt{\Large\frac{lcosθ}{g}}\)となります。
---------------------------
いかがでしたか?
結果的に、式の形も答えも同じになりますが、運動方程式と力のつりあい式とでは、それぞれの式の持つ意味合いが違います。
このように、観測者の状況と、観測者にはたらく力などを区別して考えておくと、今後物理の問題を解く上で間違いが少なくなるので、頭に入れておいてください。