高校物理の中でも1、2を争うほど有名な運動方程式を紹介します。
<運動方程式>
ある物体の質量を\(m[kg]\)、加速度を\(a[m/s^2]\)、物体にかかる(加える)力を\(F[N]\)とすると、下記の式が成り立つ。
$$ma=F$$
(\(F\)と\(a\)は共にベクトル。このため力\(F\)を加えた方向と同じ方向に、加速度が生じる)
なお、上記の式は厳密には「ニュートンの運動方程式」といいます。
というのも、運動方程式と名のつくものは、大学で習うものも含めていくつか存在するからです。
ただ、少なくとも高校物理では運動方程式を何種類も習わないので、本項でもこの形の式を「運動方程式」として進めたいと思います。
----------------------
この式を少し解釈しますと、質量と加速度をかけたものと、加える力が等しくなっています。
つまり、質量が一定であれば、加える力が大きくなるほど加速度も大きくなるということです。
また、\(ma\)=\(F\)より\(a\)=\(\frac{F}{m}\)なので、加える力が一定であれば、質量が大きくなるほど加速しにくいことも示しています。
ピンポン玉とボーリングの玉をそれぞれ同じ力で動かす場合、軽いピンポン玉の方がはるかにスピードに乗りやすいですよね。
どのような時に使う?
名前のとおり、運動方程式は物体などが運動している時に使います。
静止している物体には使いません。
静止している物体に使うのは、「力のつり合い式」です。
仮に静止している物体に運動方程式を使うとして、静止している物体は加速度がありませんから\(a\)=0、物体にはたらく力はつり合っているので\(F\)=0、結局両辺が0となって、何も意味を持ちません。
もっとも実際の問題では、運動方程式と、力のつり合い式の両方を使って解いていくパターンが多くなっています。
運動方程式を解く順序
●物体にはたらく力を全て書き出す
●物体の力のつり合い式を立てる
●「物体の運動方向を正」として、運動方程式を立てる
●二つ以上の運動方程式は、連立方程式として解く
大切なのは、物体ははたらいている力が大きい方に動くということです。
求めたいものによって運動方程式の立て方も違いますので、以下の具体例を参考にしてもらえればと思います。
運動方程式の具体例
定滑車につり下げられた二つの物体の運動

それぞれの物体にはたらく力は、図のようになります。
ここで、\(M\)<\(m\)なので物体Aは上がり、物体Bは下がります。
物体Aが上向きに運動するのは、上向きの力(\(T\))の方が大きいからです。
よって、物体Aの運動方程式は、
\(Ma\)=\(T\)-\(Mg\)・・・・・①
物体Bが下向きに運動するのは、下向きの力(\(mg\))の方が大きいからです。
よって、物体Bの運動方程式は、
\(ma\)=\(mg\)-\(T\)・・・・・②
①と②の左辺同士、右辺同士をそれぞれ足し合わせると、
\((M+m)a\)=\((m-M)g\) (\(T\)を消すことができます。)
\(∴ a\)=\(\frac{(m-M)g}{M+m}\)
「これは物体AとBどっちの加速度?」と思うかもしれませんが、Aの加速度でもあり、Bの加速度でもあります。
二つの物体は糸でつながれているので、加速度は全く同じです。
(糸でつながれた物体の運動でも、摩擦力と絡めた問題を紹介しています。)
物体の運動(なめらかな斜面上)
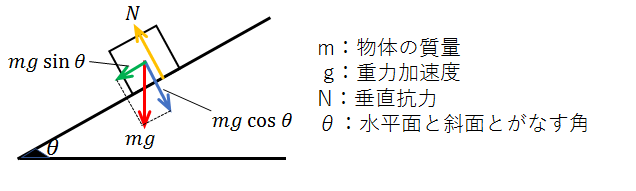
物体にはたらく力は、図のようになります。
斜面を滑り降りている時、物体の運動方程式は、
\(ma\)=\(mgsinθ\)
斜面を昇っている時、物体の運動方程式は、
\(ma\)=-\(mgsinθ\)
物体にはたらく力は重力の斜面方向の成分ですが、昇っている時は、この成分は物体の運動方向と真逆なので、マイナスがつきます。
物体の運動(あらい斜面上)
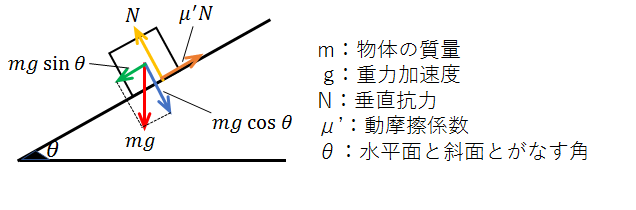
物体にはたらく力は、図のようになります。
物体が運動している時にはたらく摩擦力を動摩擦力といい、動摩擦係数と垂直抗力の積で表します。
動摩擦力は、物体が運動する向きとは、常に逆向きにはたらきます。
よって、斜面を滑り降りている時、物体の運動方程式は、
\(ma\)=\(mgsinθ\)-\(μ'mgcosθ\)
斜面を昇っている時、物体の運動方程式は、
\(ma\)=-\(mgsinθ\)-\(μ'mgcosθ\)
昇っている時、重力の斜面方向の成分と動摩擦力は、どちらも物体の運動方向と真逆なので、マイナスがつきます。
なお、斜面に垂直にはたらく力は、垂直抗力\(N\)と、重力の斜面に垂直な成分\(μ'mgcosθ\)ですが、これらは物体の運動方向と垂直なので、常につり合っています。
このため、運動方程式中の動摩擦力を表す\(μ'N\)は、\(μ'mgcosθ\)と書けるのです。
※図における摩擦力の向きは、物体が斜面を滑り降りている場合の向きを描いています。
----------------------
物理の問題では物体は様々な状況下にありますが、運動する方向によって、はたらく力の向きも変わってきます。
運動方程式の形自体はシンプルですが、実際に問題を解く際は物体にはたらく力を全て書き出すことと、物体の運動状況を把握することが、とても大切になってきます。