万有引力は、重力や静電気力と同じ保存力の仲間なので、位置エネルギーをもっています。
今回は、万有引力の位置エネルギーについて、紹介していきたいと思います。
位置エネルギーとは
はじめに、位置エネルギーの簡単なおさらいです。
位置エネルギーは力学的エネルギーのひとつであり、物体の位置によって決まるエネルギーでした。
例えば、教科書にもよく出てくる「重力による位置エネルギー\(mgh\)」は、高さ\(h\)の地点にある質量\(m\)の物体がもっているエネルギー、とされています。
なお、位置エネルギーには必ず位置の基準となる点があり、大切なのは、この基準点はどこにとっても良いということです。
上記のように重力による位置エネルギーが\(mgh\)となるのは、地上(高さ0)を基準点としているからです。
逆に高さ\(h\)の地点を基準点とした場合、高さ\(h\)における位置エネルギーはゼロ、地上における位置エネルギーは\(-mgh\)となります。

このようにどこにとっても良い基準点ですが、単に地上にとった方がややこしくないので、そうしていただけのことです。
万有引力による位置エネルギー
万有引力の位置エネルギーですが、これは基準点を無限遠にしている場合がほとんどです。
理由は重力による位置エネルギーの場合と同じで、計算をしていく上でややこしくないからです。
ちなみに重力による位置エネルギー\(mgh\)は、重力\(mg\)を\(h\)で積分し、積分定数Cをゼロとすることで求められます。
これと同じようにして、万有引力による位置エネルギーを求めてみましょう。
------------------------------
万有引力と重力の記事でも紹介してますように、質量\(M\)、\(m\)の2物体間の距離を\(r\)、万有引力定数を\(G\)とすると、物体間にはたらく万有引力の大きさ\(F\)は\(G\Large\frac{Mm}{r^2}\)と表されます。

\(G\Large\frac{Mm}{r^2}\)=\(GMm×r^{-2}\)なので、これを\(r\)で積分すると、
\(-GMm×r^{-1}\)+\(C\)
=\(-G\Large\frac{Mm}{r}\)+\(C\)(Cは積分定数)
となります。
ここで、C=0とした場合を万有引力による位置エネルギー\(U\)と仮定すると、\(U\)が0になるのは、\(r\)が無限大\(∞\)の時です。
これはすなわち、\(r\)=\(∞\)の地点が基準となっていることを示しています(位置エネルギーが0なので)。
よって、万有引力による位置エネルギーも、重力の場合と同じくC=0とした場合であり、あらためて書くと、
\(U\)=\(-G\Large\frac{Mm}{r}\)
となります。
万有引力による位置エネルギーを求めてみましたが、マイナスの符号がついているのは、基準点を無限遠にとったことと、万有引力を積分したことが理由です。
基準が無限遠ではなかったら?
試しに、無限遠以外を基準にとって、万有引力による位置エネルギーを求めてみましょう。
仮に、地表面(半径\(R\)、質量\(M\)の地球の地面)からの距離が\(R\)の点を基準としてみます。
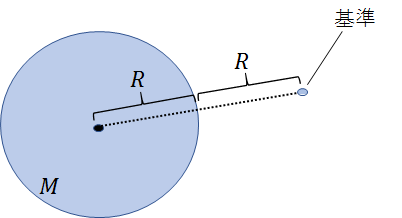
先程と同じように、万有引力\(G\Large\frac{Mm}{r^2}\)を\(r\)で積分すると、
\(-G\Large\frac{Mm}{r}\)+\(C\)(Cは積分定数)・・・・・①
となります。
基準点の位置エネルギーは、①の\(r\)に地球の中心からの距離\(2R\)を代入して、\(-G\Large\frac{Mm}{2R}\)+\(C\)です。
基準点では位置エネルギーがゼロになるので、
\(-G\Large\frac{Mm}{2R}\)+\(C\)=0
\(C\)=\(G\Large\frac{Mm}{2R}\)
よって、地表面から距離\(R\)の点を基準に選んだ時の万有引力による位置エネルギー\(U\)は、
\(U\)=\(-G\Large\frac{Mm}{r}\)+\(G\Large\frac{Mm}{2R}\)・・・・・②
と表すことができます。
この式を使って、質量\(m\)の物体がもつ、万有引力による位置エネルギーを求めてみましょう。
地表から距離\(\Large\frac{R}{2}\)離れた点A
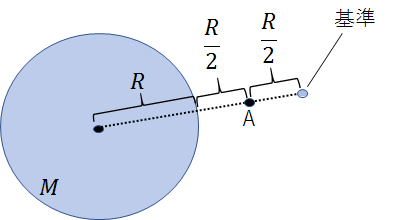
地球の中心からは\(\Large\frac{3R}{2}\)離れていますので、②式の\(r\)に\(\Large\frac{3R}{2}\)を代入すると、
\(U\)=\(-\Large\frac{2GMm}{3R}\)+\(\Large\frac{GMm}{2R}\)
=\(-\Large\frac{4GMm}{6R}\)+\(\Large\frac{3GMm}{6R}\)
=\(-\Large\frac{GMm}{6R}\)・・・・・③
地表から距離\(\Large\frac{3R}{2}\)離れた点B
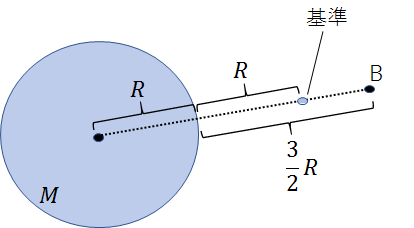
地球の中心からは\(\Large\frac{5R}{2}\)離れていますので、②式の\(r\)に\(\Large\frac{5R}{2}\)を代入すると、
\(U\)=\(-\Large\frac{2GMm}{5R}\)+\(\Large\frac{GMm}{2R}\)
=\(-\Large\frac{4GMm}{10R}\)+\(\Large\frac{5GMm}{10R}\)
=\(\Large\frac{GMm}{10R}\)・・・・・④
------------------------------
位置エネルギーを求めることができましたが、③はマイナス、④はプラスの値となってしまいました。
このように無限遠以外を基準にとると、距離が基準より大きいか小さいかによって、位置エネルギーの符号が変わってしまうのです。
ちなみに無限遠を基準にとる場合は、位置エネルギーは常にマイナスの値で、符号が変わりません(試しに計算してみてください)。
以上のことから、万有引力による位置エネルギーの基準点が無限遠となっているのは、符号が変わらないので、ややこしくないからだと言えます。
※基準をどこにとるかは、好みの問題もあるので自由ですが、もしも問題文に「無限遠を基準とする」などと書かれていたら、それに従うようにしてください。