ある物体を投げて(発射して)、地球のまわりをまわらせるために必要な初速度を第1宇宙速度といいますが、これと同じ概念として「第2宇宙速度」というものがあります。
第2宇宙速度とは
第2宇宙速度とは、地球の重力を振り切るために必要な、地表における初速度(引用:wikipedia)のことです。
つまり、地上から投げた物体が、地球のまわりをまわることなく地球を離れていってしまうための、最小の初速度をいいます。
人工衛星のように、物体が地球のまわりをまわるのは地球の重力の影響ですが、打ち上げる時に第2宇宙速度以上の速度を与えると、重力に勝って遥か彼方へ飛んでいってしまうのです。
色々な資料では、「第2宇宙速度は第1宇宙速度の\(\sqrt{2}\)倍」とされています。
(第1宇宙速度が\(\sqrt{gR}\)なので、第2宇宙速度は\(\sqrt{2gR}\))
これはこれで覚えてしまえば問題ないのですが、せっかくなので導き方も以下で説明します。
スタートは力学的エネルギー保存則
万有引力は保存力の仲間なので、力学的エネルギー保存則が成り立ちます。
ここで、質量\(M\)、半径\(R\)の地球と、そのまわりを運動する質量\(m\)の物体を考えてみましょう。

図のように、地表から物体を初速度\(v_0\)で打ち上げた場合、地表における運動エネルギーは\(\Large\frac{1}{2}\)\(mv^2_0\)、万有引力による位置エネルギーは、無限遠を基準とすると\(-G\Large\frac{Mm}{R}\)と表されます。
よって、地表における物体の力学的エネルギーは、
\(\Large\frac{1}{2}\)\(mv^2_0\)\(-G\Large\frac{Mm}{R}\)・・・・・①
です。
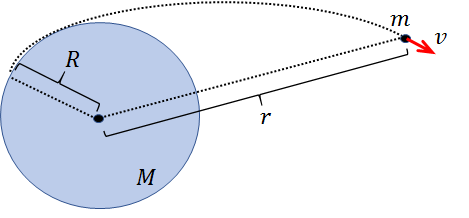
一方、打ち上げた後、地球の中心から距離\(r\)だけ離れた地点の物体の速度を\(v\)とすると、物体の運動エネルギーは\(\Large\frac{1}{2}\)\(mv^2\)、万有引力による位置エネルギーは\(-G\Large\frac{Mm}{r}\)と表されます。
よって、この地点における力学的エネルギーは、
\(\Large\frac{1}{2}\)\(mv^2\)\(-G\Large\frac{Mm}{r}\)・・・・・②
です。
力学的エネルギー保存則より①=②なので、
\(\Large\frac{1}{2}\)\(mv^2_0\)\(-G\Large\frac{Mm}{R}\)=\(\Large\frac{1}{2}\)\(mv^2\)\(-G\Large\frac{Mm}{r}\)
・・・・・③
が成り立ちます。
ところで、物体の勢いが地球の重力に勝つことが明確なのは、どういった条件でしょうか?
発射後の物体の位置\(r\)は刻々と変わりますが、例えば\(r\)が\(3R\)とか\(5R\)という具体的な値だと、本当に勝つかどうかは怪しいところです。
ポイントは、物体がとてもとても遠く(=無限大の地点)に行った状態を考えます。
このような遠くの位置でも、仮に物体がまだ速度をもっているとなると、地球の重力を振り切って遥か彼方へ飛んでいきそうです。
そのような観点から、地球の重力を振り切る条件は、
\(r\)=\(∞\)の時に\(v\)≧0
つまり、
\(r\)=\(∞\)の時に\(\Large\frac{1}{2}\)\(mv^2\)≧0
となります。
これを③式に適用していくと、まず右辺の\(r\)が\(∞\)の時、右辺の位置エネルギーはゼロとなります。
\(\Large\frac{1}{2}\)\(mv^2_0\)\(-G\Large\frac{Mm}{R}\)=\(\Large\frac{1}{2}\)\(mv^2\)+0
また、条件の\(\Large\frac{1}{2}\)\(mv^2\)≧0は、(左辺)≧0と同じことです。
よって、
\(\Large\frac{1}{2}\)\(mv^2_0\)\(-G\Large\frac{Mm}{R}\)≧0
\(\Large\frac{1}{2}\)\(mv^2_0\)≧\(G\Large\frac{Mm}{R}\)
\(v^2_0\)≧\(\Large\frac{2GM}{R}\)
\(v_0\)≧\(\Large\sqrt{\frac{2GM}{R}}\)
\(GM\)=\(gR^2\)の関係式を代入すると、
\(v_0\)≧\(\sqrt{2gR}\)
物体はこの条件の時に重力に勝つので、条件の最小速度がすなわち第2宇宙速度であり、
\(v_0\)=\(\sqrt{2gR}\)
となります。