ケプラーの法則とは、1619年にドイツのヨハネス=ケプラーによって発見された、惑星の運動に関する法則です。
ケプラーの第1法則
惑星は、太陽を焦点のひとつとする楕円軌道上を運動する。
現在は当たり前になっている「惑星が太陽のまわりをまわる」運動を少し具体的に書いたものです。

一般的に楕円には焦点が二つあり、そのうちのひとつが太陽とのことですが、もう片方の焦点の位置には何もありません。
また、軌道となる楕円は、ほぼ円に近い形をしています。
ただし、太陽は軌道の中心ではなく、あくまで焦点のひとつということに注意してください。
ケプラーの第2法則
惑星と太陽とを結ぶ線分が、単位時間に描く面積は一定である。
楕円軌道上を動く同じ惑星が、同じ時間で点A→B、点C→Dへとそれぞれ移動したとします。

太陽の位置を点Oとすると、移動し終えるまでに線分OA、OCがそれぞれ通過した部分の面積が、等しいということです。
図の場合、\(S_1\)=\(S_2\)となります。
ここで、太陽から惑星までの距離を\(r\)、惑星の速度を\(v\)として、通過した部分の面積\(S_1\)を求めてみます。
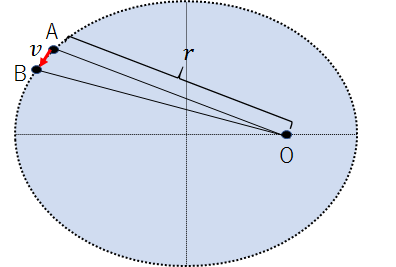
軌道は楕円なので、点Aから点Bまでの経路は曲がっています。
ですが、点Aと点Bの距離がごくわずかな場合、点Aからまっすぐ進んだ場合の点をB'とすると、\(S_1\)は、三角形OAB'の面積と同じとみなすことができます。
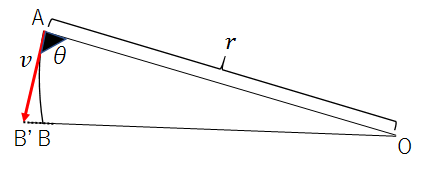
線分OAとAB'がなす角を\(θ\)とすると、三角形OAB'の底辺は\(r\)、高さは\(vsinθ\)なので、求める面積は、\(\Large\frac{1}{2}\)\(rvsinθ\)となります。
この中で、惑星の移動中に刻々と変化するのは、\(r\)と\(v\)です。
面積は常に一定ですので、\(r\)が小さいと\(v\)は大きくなり、逆に\(r\)が大きいと\(v\)は小さくなります。
これはつまり、太陽に近いところでは動きが速くなり、太陽から遠いところでは動きが遅くなることを示しています。
ケプラーの第3法則
惑星の公転周期の2乗は、楕円の軌道長半径の3乗に比例する。
軌道長半径とは、楕円の場合、長軸方向の半径のことです。
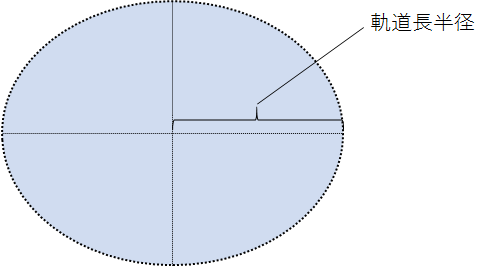
軌道長半径を\(a\)、公転周期を\(T\)とおいて式で表すと、
\(T^2\)=\(ka^3\)
となります。
この式において、\(a\)が大きくなるとその分\(T\)も大きくなります。
\(a\)が大きいということは、軌道となっている楕円そのものが大きいということなので、太陽から遠い惑星ほど、太陽のまわりを一周するのに時間がかかるということです。
(かかる時間は、水星→金星→地球→火星→木星→土星→天王星→海王星の順に増えていきます。)