ロケットの一部が分裂する問題

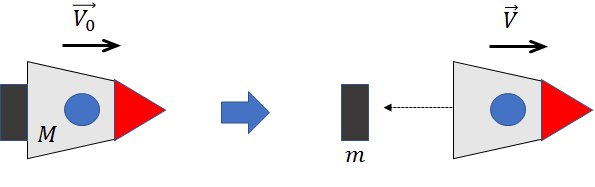
噴射時、ロケットは燃料に力を及ぼします(この力によって燃料は飛んでいきます)。

逆にロケット自身も、燃料に及ぼした力と同じ力を受けます。

噴射によって、ロケットと燃料それぞれにはたらく力はこの「互いに及ぼし合う力」のみなので、噴射前と噴射後とで運動量は一定です。

まずは噴射前と噴射後の質量と速度を元に、運動量保存則の式を立ててみましょう。

＜噴射前＞

ロケットと燃料は、まだ一体となって進んでいます。

よって、質量と速度は問題文にある通り、\(M\)と\(\overrightarrow{V_0}\)です。

＜噴射後＞

噴射後のロケットは、離れた燃料分だけ質量が減るので、ロケットの質量は\(M－m\)、燃料の質量は\(m\)です。

速度は、ロケットについては問題文より\(\overrightarrow{V}\)、燃料については特に記載が無いので、仮に\(\overrightarrow{v}\)とおきましょう。

よって、運動量保存則の式は、

\(M\)\(\overrightarrow{V_0}\)＝(\(M－m\))\(\overrightarrow{V}\)＋\(m\)\(\overrightarrow{v}\)

となります。

先述したとおり、ある物体の相対速度はその物体を別の観測者から観測したときの速度で、ロケットから燃料を観測した場合、\(\overrightarrow{u}\)＝\(\overrightarrow{v}\)－\(\overrightarrow{V}\)であることから、燃料の速度\(\overrightarrow{v}\)は、\(\overrightarrow{v}\)＝\(\overrightarrow{u}\)＋\(\overrightarrow{V}\)と表されます。

これを\(\overrightarrow{v}\)に代入して、あらためて運動量保存則の式を書くと、

\(M\)\(\overrightarrow{V_0}\)＝(\(M－m\))\(\overrightarrow{V}\)＋\(m\)(\(\overrightarrow{u}\)＋\(\overrightarrow{V}\))・・・①

となります。

展開して整理すると、

\(M\)\(\overrightarrow{V_0}\)＝\(M\overrightarrow{V}\)－\(m\overrightarrow{V}\)＋\(m\overrightarrow{u}\)＋\(m\overrightarrow{V}\)

＝\(M\overrightarrow{V}\)＋\(m\overrightarrow{u}\)

\(M\)\(\overrightarrow{V}\)＝\(M\)\(\overrightarrow{V_0}\)－\(m\overrightarrow{u}\)

よって、噴射後のロケットの速度\(\overrightarrow{V}\)は、

\(\overrightarrow{V}\)＝\(\overrightarrow{V_0}\)－\(\Large\frac{m}{M}\)\(\overrightarrow{u}\)

です。

速度が絡む時は符号に注意

問題文のシチュエーションでは、噴射後、ロケットと燃料が互いに逆向きに進んでいますよね。

これは、相対速度の項目で説明した例２に相当し、仮に右向きを正とすると、噴射後のロケットから見た燃料の速度はマイナスとなることに注意してください。

最後に、問題文に具体的な数値を入れて、噴射後のロケットの速度を求めてみましょう。

数値については、適当に選びました。

あくまで説明のためなので、ロケットの質量が本当に2000[kg]程度なのかは、わかりません(笑)。

さて、ロケットから見た燃料の速度が負の値なので、これはロケットの進む方向を正としています。

上記で求めた\(\overrightarrow{V}\)＝\(\overrightarrow{V_0}\)－\(\Large\frac{m}{M}\)\(\overrightarrow{u}\)の式に\(\overrightarrow{V_0}\)＝50、\(M\)＝2000、\(m\)＝1000、\(\overrightarrow{u}\)＝－10を代入すると、

\(\overrightarrow{V}\)＝\(50\)－\(\Large\frac{1000}{2000}\)×\((－10)\)＝\(55\)

噴射後、ロケットの速度は55[m/s]にアップすることがわかります。

噴射時に燃料に及ぼした力を、自分自身も受けたからです。