図のように、質量\(m\)のおもりをつり下げると\(l\)だけ伸びるばねがあります。

このばねの両側に糸を付け、さらにその先に、なめらかな滑車を通して質量\(m\)のおもりを取り付けてみます。
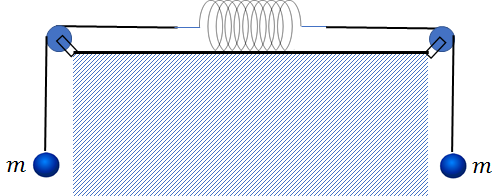
なお、重力加速度は\(g\)とします。
このとき、ばねは全体でどれだけ伸びるでしょうか?
--------------------------
ばねを\(l\)だけ伸ばすおもりが両端にぶら下がっているから、全体の伸びは\(2l\)だ。
もしかすると、このようにイメージされたでしょうか?
正解は\(l\)です。
もしも間違えた方は、以下の説明を読んでみてください。
力のつり合いを考えてみる
両端におもりがぶら下がった状態だとイメージしにくいので、左端はおもりの代わりに頑丈なポールがあり、糸がつながっていると仮定します。
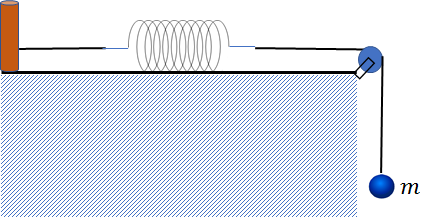
この状態において、ばねの右端に着目してみます。
下向きには重力\(mg\)がはたらいていますね。
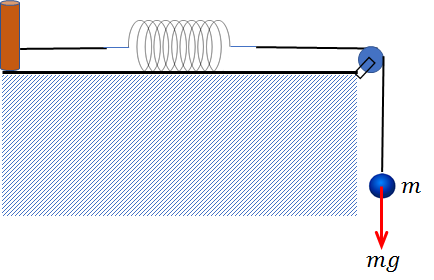
これは、天井に鉛直につるされたばねの下に、質量\(m\)のおもりがぶら下がっている状況と全く同じです。
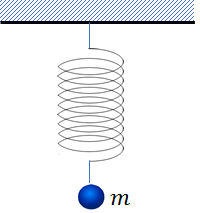
ポールが、天井に該当します。
そしてこの場合、初めの条件よりばねは\(l\)だけ伸びています。
また、糸とばね、そしてポールは全てつながっていますので、左端の「糸がポールを引っ張る力」も\(mg\)です。
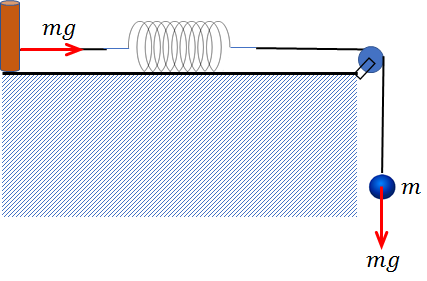
鉛直につるされたばねの場合だと、ここに該当します。
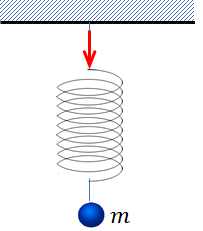
つまり、右端に加わった力\(mg\)によって、最終的にポールにも右向きに\(mg\)の力が加わっています。
そして、ポールは同じ力\(mg\)で、糸を左向きに引っ張り返しています(作用・反作用の法則)。
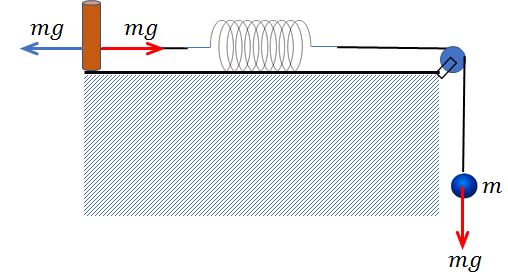
なお、状況は何も変わっていないので、ばねの伸びは\(l\)のままです。
以上のことから、右端のおもりにはたらく力と、ポールが糸を低く力は同じです。
\(mg\)とは、そもそも質量\(m\)のおもりにはたらく重力なので、ポールの代わりに質量\(m\)のおもりをつり下げても全く同じです。

初めの状況になりましたね。
結局この状況も、天井に鉛直につるされたばねの下に質量\(m\)のおもりがぶら下がっている状況と意味は同じ、ということです。
したがって、ばねの伸びは\(l\)となります。
--------------------------
もしも、左端につり下げるおもりの質量が\(\frac{m}{2}\)だったらどうなるでしょう?
この場合、力のつり合いが保たれないので、全体が右に移動してしまいます。
両端のおもりは、ばねを両端からそれぞれ\(l\)だけ伸ばしているのではなく、片端のおもりにはたらく力によって移動しないよう、支える役割を担っているのです。