ばねの性質とフックの法則

何も手を加えてない状態のばねの長さを、「自然長」といいます。

自然長からばねを伸ばして手を離すと、勢いよく縮みます。

逆に、縮ませて手を離すと、勢いよく伸びます。

どちらの場合も、ばねは元の長さ(自然長)に戻ろうとしているからです。

手応え＝弾性力

例えば、自然長のばねを手でそっと触れた状態と、手で力を加えて伸ばした状態とでは、感じる手応えが違います。

なぜなら、伸ばされたばねは一生懸命元の長さに戻ろうとして、力を発揮しているからです。

このように、変形させられた物体が元に戻ろうとしてまわりに及ぼす力を、「弾性力(だんせいりょく)」、あるいは「復元力(ふくげんりょく)」といいます。

ばねの場合は、どちらかと言えば「弾性力」の方をよく使います。

弾性力は、ばね定数と、ばねの自然長からの変位を用いて、下記のように表されます。

中学で習った一次関数y＝axの形と同じですね。

ばねに加えた力とばねの伸びは比例関係にあり、これを「フックの法則」といいます。

なお、式中の\(k\)は比例定数(ばね定数)で、ばねの伸びにくさや縮みにくさを表し、ばねによってそれぞれ違います。

中には、弾性力がばねの伸び縮みに比例しないばねもあるのですが、少なくとも高校物理の範囲では、比例するようなばねを扱うので安心してください(笑)。

なぜマイナスがつく？

フックの法則の式を見ると、\(kx\)の前にマイナスがついていますよね。

これは、弾性力がはたらく向きが関係しています。

例として、ばねを自然長から\(x\)だけ伸ばす状況を考えてみましょう。

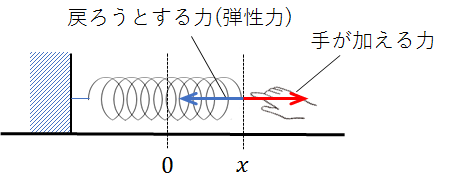
図のように右向きに伸ばしたとすると、ばねは元に戻ろうとして左向きに力(＝弾性力)を発揮します。

なぜならこの場合、左向きが、自然長に戻れる向きだからです。

つまり、伸ばす向きと弾性力の向きは、互いに真逆となります。

\(kx\)にマイナスがついているのは、弾性力が、変位とは逆向きにはたらくことを示しているのです。

※変位とは、最初の位置からどれだけ変わったかを表す量なので、ばねが\(x\)だけ伸びても、\(x\)だけ縮んでも、変位は\(x\)です。

弾性力は保存力

「保存力」と「力学的エネルギー保存則」では、保存力は下記のようなものであると紹介しました。

弾性力も、こうした保存力の仲間です。

ただ、同じ保存力である重力と違い、弾性力は物体を移動させる空間ではなく、ばね自身や、ばねに取り付けられた物体などに対してはたらきます。

なので弾性力の場合、物体の移動経路というよりは、「自然長の位置を中心に3回往復しても20回往復しても、トータルの仕事は同じ」という解釈で構いません。

重力とは少し性質が違いますが、同じ保存力だということは、覚えておいてください。