振り子の一種である「円錐振り子」の力のつり合い式について考察をまとめましたので、参考にしてみてください。
鉛直方向には運動しないことを利用する
円錐振り子とは、質量が無視できる糸の一端を固定し、他端に質点とみなせるおもりをつけた振り子のうち、おもりが水平面内を円運動するものを指します。

おもりの質量を\(m\)、重力加速度を\(g\)として、この振り子にはたらく力を図示してみます。
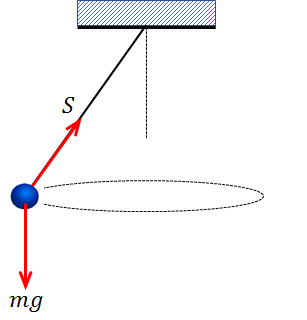
\(mg\)・・・おもりにはたらく重力
\(S\)・・・糸の張力
おもりは水平面内を運動するので、鉛直方向には運動しません。
ゆえに、鉛直方向の力はつり合っていると言えます。
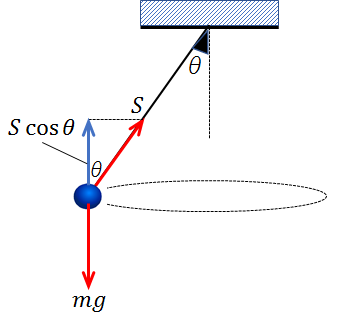
糸が鉛直線から\(θ\)だけ傾いているとすると、張力の鉛直成分は\(Scosθ\)なので、鉛直方向の力のつり合い式は、
\(Scosθ\)=\(mg\)・・・・・①
となります。
重力を分解する方法は使えるのか?
上記では張力を分解しましたが、逆に重力の方を分解して、糸の張力方向の力のつり合い式を立てることはできるのでしょうか?
結論から言えば、できます。
なぜなら軽くて伸び縮みしない糸であれば、おもりは張力の方向に運動しないからです。
ただこの場合は、もうひとつ別の力も考慮しないといけません。
張力の水平成分\(Ssinθ\)です。
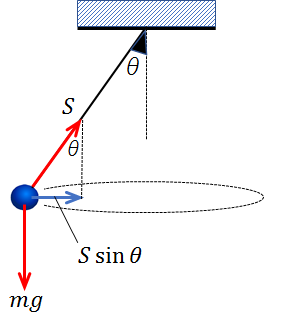
\(Ssinθ\)は、円運動の特徴である向心力(円の中心に向かう力)に該当し、\(S\)と\(mg\)の合力にあたります。
また、一般的に円運動をしている物体に観測者が乗っている場合、観測者には向心力と真逆の向きに「遠心力」がはたらきます。
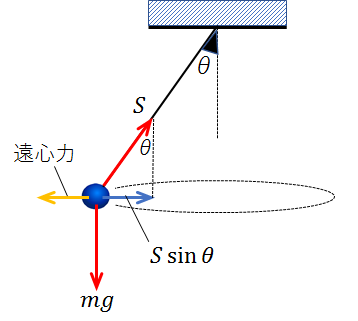
⚫遠心力
今回の例では与えられていませんが、円運動をする円の半径を\(r\)、角速度を\(ω\)とすると、\(mrω^2\)と表されます。
ややこしいですが、遠心力は「観測者がおもりに乗っている場合」に感じる力で、このような場合、観測者から見ておもりは静止していますから、向心力と遠心力がつり合っているように見えます。
したがって振り子全体で見ると、遠心力と\(S\)と\(mg\)の合力が「ゼロ」となっています。
---------------------------------
試しに、遠心力\(mrω^2\)が与えられていたとして、遠心力を分解してつり合い式を立てて見ましょう。
遠心力と重力を糸の張力方向に分解すると、下記のようになります。
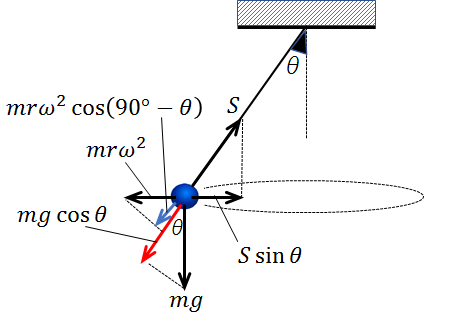
よって、糸の張力方向の力のつり合い式は、
\(S\)=\(mgcosθ+mrω^2cos(90°-θ)\)
\(S\)=\(mgcosθ+mrω^2sinθ\)・・・②
また、張力に垂直な方向についても力を分解し、つり合い式を立てると、
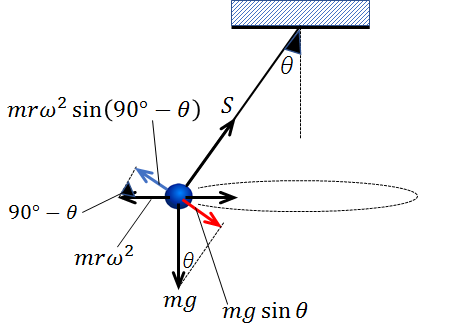
\(mgsinθ\)=\(mrω^2sin(90°-θ)\)
\(mgsinθ\)=\(mrω^2cosθ\)・・・③
●三角比の公式
sin(90°-θ)=cosθ
cos(90°-θ)=sinθ
③より\(mrω^2\)=\(\Large\frac{mgsinθ}{cosθ}\)であるから、これを ②に代入すると、
\(\Large\frac{mgsinθ・sinθ}{cosθ}\)+\(mgcosθ\)=\(S\)
両辺に\(cosθ\)をかけると、
\(mgsin^2θ\)+\(mgcos^2θ\)=\(Scosθ\)
\(mg(sin^2θ+cos^2θ)\)=\(Scosθ\)
\(sin^2θ\)+\(cos^2θ\)=1より、
\(mg\)=\(Scosθ\)
①の結果と一致しましたね。
計算は楽な方がいい
結局、力のつり合い式を鉛直方向と張力方向どちらで立てても、結果は同じであることがわかりました。
ただ、後者は向心力や遠心力を考慮しなければならないので、計算が面倒な上、ミスをする可能性も高くなるかと・・・。
解き方に決まりはありませんが、円錐振り子の力のつり合い式は、鉛直方向で立てた方が(張力を分解してあげた方が)比較的楽に結果を求められることを覚えておいてください。