円運動とは、物体が円の円周上を進む運動のことです。
このうち速さが一定の場合を「等速円運動」といいます。
ちなみに、物体が真っすぐ進んでいる場合は「直線運動」です。
特に速さが一定である「等速直線運動」をしている物体の移動距離は、速さ×時間で求められましたね。

上の図からも分かるように、二つの運動の大きな違いはスタート地点に戻ってくるかどうかです。
直線運動は、物体に力を加えるなどして向きを変えない限り、スタート地点からどんどん離れていきます。
これに対して円運動は、円を1周するとまたスタート地点に戻ります。
この特徴はとても重要なので、覚えておいて下さい。
角速度と速さ
円運動では、これまで見ることの無かった「角速度」という言葉が出てきます。
角速度とは、円運動している物体が1秒間にどのくらいの角度進んだかを表しており、
量記号は\(ω\)、単位は[rad/s]です。
「rad」は(ラジアン)と読み、角度を表す表記の一つです。
図のような半径\(r\)[m]の円において、円弧の長さも半径と同じ\(r\)[m]となる時の中心角を、「1ラジアン」と定義しています。

この定義があるおかげで、半径と中心角から、円弧の長さを求めることができます。
上の図では半径\(r\)[m]、中心角1[rad]の円弧の長さが\(r\)[m]なので、
つまりは円弧の長さ[m]=半径(\(r\)[m])×中心角(1[rad])です。
これを一般的な形で表すと、半径\(r\)、中心角\(θ\)[rad]の円弧の長さ\(l\)は、
\(l\)=\(r\)\(θ\)・・・①
で求められます。
これまでは「°」(度)を使って表していたかもしれませんが、高校の数学や物理ではラジアンを使うようになりますので、少しずつ慣れていってください。
ちなみに「度」と「ラジアン」の間には、一例として次のような関係があります。
30°= \(\Large\frac{π}{6}\)[rad]、60°= \(\Large\frac{π}{3}\)[rad]、90°= \(\Large\frac{π}{2}\)[rad]
180°= \(π\)[rad]、270°= \(\Large\frac{3π}{2}\)[rad]、360°= \(2π\)[rad]
ここで、物体が下図のスタート地点から円運動を始め、\(t\)秒間で角度\(θ\)[rad]だけ進んだとします。
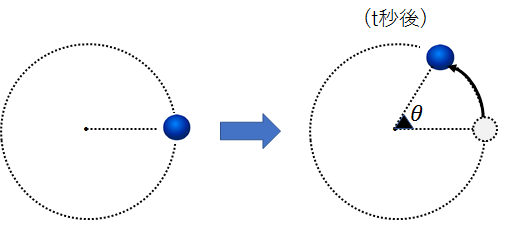
この時の角速度\(ω\)は、進んだ角度をかかった時間で割って、
\(ω\)[rad/s]=\(\Large\frac{θ}{t}\)・・・②
となります。
--------------------------------
次に、物体が等速円運動をしている時の、速さを求めてみましょう。

物体が\(t\)秒間に進んだ距離は図の赤色の部分なので、これを\(l\)[m]とすると、
①式の関係より、\(l\)=\(rθ\)と表すことができます。
物体の速さ\(v\)は、この距離をかかった時間で割ればいいので、
\(v\)[m/s]=\(\Large\frac{l}{t}\)=\(\Large\frac{rθ}{t}\)・・・③
②を変形すると\(θ\)=\(ωt\)でなので、これを③に代入して、最終的に\(v\)=\(r\)\(ω\)となります。
ここで、ちょっとした問題をやってみましょう。
ある物体が、半径2[m]の円周上を2秒かけて1周した。
なお、物体は等速円運動をしたものとする。
(1)このときの角速度を求めよ。
(2)この物体の速さを求めよ。
(解答)
(1)角速度とは、「1秒間に進んだ角度」のことでした。
今回、物体は2秒かけて1周したので、
2秒かけて進んだ角度は360度、ラジアンで表すと\(2π\)[rad]です。
よって求める角速度は、\(\Large\frac{2π}{2}\)=\(π\)[rad/s]となります。
(2)物体が進んだトータルの距離は、半径2[m]×中心角\(2π\)=\(4π\)です。
2秒でこの距離を進んだので、求める速さは、\(\Large\frac{4π}{2}\)=\(2π\)[m/s]となります。
※進んだ距離を出す際に、先程の\(l\)=\(r\)\(θ\)の関係を使いましたが、もちろんおなじみの「円周=半径×2×\(π\)」の公式でも出すことができます。
結果を見ると、角速度と物体の速さはそれぞれ違う値になりましたね。
つまり、角速度と物体の速さは別物ということです。
間違えやすいですが、角速度=物体の速さではないことに注意してください。
あくまで角速度は「1秒間に進んだ角度」、速さは「1秒間に進んだ距離」です。
等速円運動の周期
物体が等速円運動している時、1周するのにかかる時間を周期といい、量記号\(T\)、単位[s](秒)で表します。
なぜ周期というものが存在するかというと、等速円運動をしている物体は、決まった時間間隔でスタート地点を通過するからです。
例えば、スタートしてから3秒後に1周、6秒後に2周、9秒後に3周したとすると、
1周するのに3秒かかっているので、すなわち周期は3[s]ということです。
また、2周するのに6秒かかっているので、周期は\(\Large\frac{6}{2}\)=\(3\)[s]でも求められます。
3周の場合も同様です。
これらの関係を一般的な式で表してみましょう。
今、ある物体が半径\(r\)[m]の円を速さ\(v\)[m/s]で等速円運動しているとします。
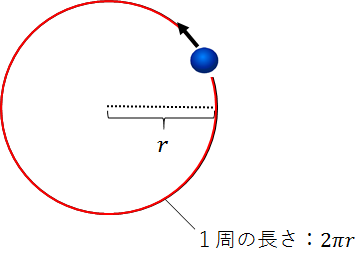
この円の1周分の長さは\(2πr\)[m]なので、1周するのにかかる時間は\(\Large\frac{2πr}{v}\)[s]です。
ここで、\(v\)=\(rω\)を代入すると、\(\Large\frac{2πr}{rω}\)=\(\Large\frac{2π}{ω}\)[s]となります。
--------------------------------
以上、円運動の基本事項について紹介しました。
これ以外の細かい点は他にもいくつかありますが、また随時紹介していきたいと思います。
基本的な事柄ですが、問題を解く際に頻繁に使うようになるので、頭の隅に入れておいて下さいね。