図のように、ある物体を水平方向に速さ\(Vo\)で壁にぶつけ、ぶつかった物体は、跳ね返って水平方向逆向きに速さ\(V\)で戻ってくるとします。
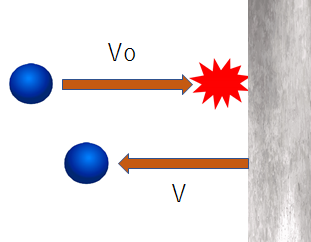
この時、\(V\)と\(Vo\)の比を反発係数(跳ね返り係数)といい、\(e\)で表します。
$$e=\frac{V}{Vo}・・・・・(1)$$
※○と○の比とは?
例えば「AとBの比」というとA:Bが一般的ですが、
「Bを1とした時のAの値」、つまりA/Bを、「AとBの比」とも言ったりします。
ただ、教科書を見ていると、
$$e=-\frac{V}{Vo}・・・・・(2)$$
のようにマイナスの符号が付いていることもあり、
$$e=\frac{|V|}{|Vo|}・・・・・(3)$$
のように\(V\)と\(Vo\)それぞれに絶対値が付いている場合もあります。
形の違う式が色々登場して混乱するかと思いますが、
書き方が違うだけで、式(1)も式(2)も「同じ反発係数を求めているもの」です。
ではなぜこのようにいくつも式があるかといいますと、
式(1)と(3)は、\(V\)と\(Vo\)が「速さ」、式(2)と(3)は、\(V\)と\(Vo\)が「速度」の場合に用いるという違いがあるからです。
速さは「大きさ」を持つもの、
速度は「大きさと向き」を持つもので、これらは完全に別物。
(「速さと速度の違い」より)
では、最初の図に対して、向きと速さを具体的に決めてみましょう。
(問)
水平方向右向きに速さ20[m/s]で進んでいる物体が、壁にぶつかって跳ね返り、水平方向左向きに速さ10[m/s]で進んだ。
このとき、物体と壁との間の反発係数を求めよ。
ただし、水平方向右向きを正とする

問題文には「速さ」と「向き」が与えられていますね。
反発係数を式(1)を使って求める場合、当てはめるものは速さですから、壁の跳ね返り係数\(e\)は、
$$e=\frac{10}{20}=0.5$$
となります。
式(2)を使って求める場合、当てはめるものは速度ですから、
壁の跳ね返り係数\(e\)は、
$$e=-\frac{-10}{20}=0.5$$
となります。
ここで、なぜ10にマイナスが付いているかといいますと、跳ね返ったことで水平方向左向き、すなわち「負」の方向に進んだからです。
速度は向きも考えなければならないので、単純に10を代入しただけでは間違いです。
---------------------------
さて、それぞれの式で反発係数が求まりましたが、大事なことがもうひとつ、
それは、
反発係数は、絶対に負の値にならない
ということです。
反発係数は、ぶつかった物体が跳ね返る度合いを示すものなので、必ず0≦\(e\)≦1の範囲をとり、\(e\)のとる値によって、それぞれ名前がついています。
\(e=1\)・・・・・弾性衝突
\(0≦e<1\)・・・・・非弾性衝突
非弾性衝突の中でも、\(e=0\)の場合を「完全非弾性衝突」といいます。
教科書によって分類の仕方は違うこともありますが、物体の状態は同じです。
これはつまり、動かない壁との衝突であれば、跳ね返った後に物体の速さが大きくなることはあり得ないとも言えます。
ちなみに、式(3)に「速さ」と「速度」両方とも当てはめることができるのは、\(V\)と\(Vo\)の絶対値を使っているからです。
たとえ\(V\)がマイナスでも、絶対値はプラスなので反発係数が負の値をとることは無くなるわけです。
ただ、問題を解くにあたって物体の「速さ」が与えられているのか、「速度」が与えられているのかは、必ず初めに確認するようにしてくださいね。
余談
物体が別の物体に衝突して速さが変わる身近なケースとしては、「野球」があります。
ピッチャーがゆっくり投げたボールをバッターが打ち返した時、ボールはすごい勢いで飛んでいきますよね。
これは、ボールが単にバットにぶつかって跳ね返っただけでなく、バットからボールに
ものすごい力が加わったために速さが変化したからです。