静止摩擦力と動摩擦力

静止摩擦力

面の上の物体を、力を加えて動かす状況をイメージしてください。

例えば、面が氷のようにつるつるであれば、ほんの少し触れただけでも物体は動き出しますが、ざらざらの場合、少し触れた程度ではほとんど動きません。

また、重い物体であれば、加える力を徐々に大きくしていくと、ある大きさを超えたところで急に動き出したりします。

この動き出すまでの間、物体にはたらいている摩擦力を「静止摩擦力」といい、加える力と逆向きにはたらきます。

静止摩擦力の大きさは、物体に加える力の大きさ(＝外力の大きさ)と同じで、物体が動き出すまでは、加える力に伴って静止摩擦力も大きくなっていきます。

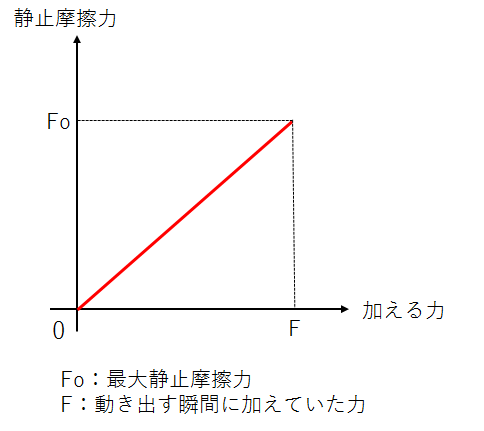
しかし、加える力が静止摩擦力が持ちこたえられる以上の大きさになると、物体は加えた力の方向に動き出します。

グラフ中の\(Fo\)ですが、これは動き出す直前の時点で物体にはたらいている静止摩擦力で、「最大静止摩擦力」といい、下記のように表します。

静止摩擦係数とは、置かれた物体と摩擦がある面との兼ね合いを示すもので、面の材質によっても様々です。

また、垂直抗力は、物体を面に押し付けている力の反作用として受ける力のことです。

したがって静止摩擦力は、

●物体が置かれている面の状態

●物体を押し付けている力

によって決まることがわかります。

※静止摩擦係数は、最大静止摩擦力を表す時に使う係数であることに、注意してください。

動摩擦力

物体が動いている間、その物体の運動方向と逆向きにはたらく摩擦力を「動摩擦力」といい、下記のように表します。

動摩擦力も静止摩擦力と同様に、

●物体が置かれている面の状態

●物体を押し付けている力

によって決まることがわかります。

この動摩擦力ですが、

●最大静止摩擦力よりも小さい

●動いている間、大きさは変わらない

といった特徴を持っています。

これらを踏まえて、物体に加える力と動摩擦力との関係をグラフに表すと、下記のようになります。

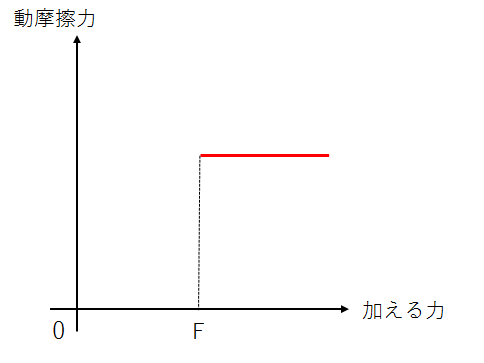
最大静止摩擦力に達するまでは、力を加えていっても物体は静止したままです。

ですが、加える力が最大静止摩擦力を超えた瞬間から物体は動き出し、面との摩擦力は動摩擦力となります。

上記のグラフが示す通り、「最大動摩擦力」というのはありません。

動摩擦力は、加える力が変化しても、物体が動いている限り常に一定であるからです。

なので、物体が動き始めた瞬間に加えていた力と同じ力を加え続けていれば、物体は等速で運動します。

物体に加える力と、動摩擦力がつり合っているからです。

しかし、物体に加える力が動摩擦力よりも大きくなれば、物体は加速します。

逆に、物体に加える力が動摩擦力よりも小さくなれば、物体は減速します。

自分自身が変わらないというのが、静止摩擦力とは大きく異なる点です。

物体が静止しているか動いているか

結局のところ、物体にはたらく摩擦力が何であるかは、その物体の運動状態によります。

なお、物体との間に摩擦が発生するような面を「あらい面」と表現することが多いので、頭の隅に入れておいてください。