(問)
長さ\(l\)の軽い糸に、質量\(m\)のおもりをつけた単振り子がある。
このおもりを、図のように糸が鉛直方向と60°の角度をなす地点まで持ち上げて静かに離したところ、おもりは振り子運動を行った。
重力加速度の大きさを\(g\)、空気抵抗は無視できるものとして、次の問いに答えよ。

(1)最下点におけるおもりの速さを求めよ。
(2)おもりが、鉛直方向とのなす角が\(θ\)の地点に達した時のおもりの速さを求めよ。
おもりにはたらく力は「重力」と「糸の張力」ですが、張力はおもりの進行方向に対して常に垂直なので、おもりに対して仕事をしません。
つまり、おもりの運動に関与している力は重力(=保存力)のみなので、おもりの力学的エネルギーは一定となります。
まず(1)ですが、初めに、離した地点(スタート地点)の力学的エネルギーを求めてみます。
力学的エネルギーは、位置エネルギーと運動エネルギーの和でした。
●位置エネルギー
まずおもりの高さを求めるために、基準点を決める必要があります。
基準点はどこに決めてもよいのですが、おもりは最下点より下にくることは無いので、最下点を位置エネルギーの基準点とすると、計算が楽になります。
おもりの高さについては、図に少し手を加えてみましょう。
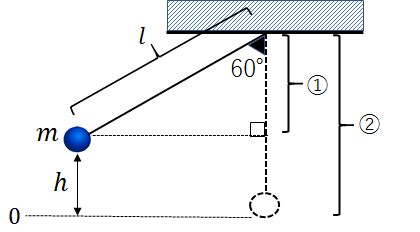
図のように水平線を引くと、スタート地点の基準点からの高さ(\(h\))は、②-①で求められます。
よって、高さは\(l-lcos60°\)=\(l-\Large\frac{l}{2}\)=\(\Large\frac{l}{2}\)であることから、
位置エネルギーは\(\Large\frac{1}{2}\)\(mgl\)となります。
●運動エネルギー
スタート地点では、まだおもりに速さがありません。
よって、運動エネルギーはゼロです。
したがって、スタート地点の力学的エネルギーは、
\(\Large\frac{1}{2}\)\(mgl\)+\(0\)=\(\Large\frac{1}{2}\)\(mgl\)・・・・・③
です。
----------------------------
続いて最下点を見ていきます。
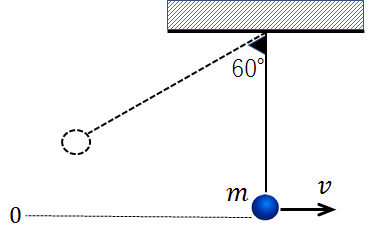
●位置エネルギー
基準点としている位置なので高さがありません。
よって、位置エネルギーはゼロです。
●運動エネルギー
最下点における速さを\(v\)とすると、\(\Large\frac{1}{2}\)\(mv^2\)です。
よって、最下点の力学的エネルギーは、
\(0\)+\(\Large\frac{1}{2}\)\(mv^2\)=\(\Large\frac{1}{2}\)\(mv^2\)・・・・・④
となります。
力学的エネルギー保存則より③=④なので、
\(\Large\frac{1}{2}\)\(mgl\)=\(\Large\frac{1}{2}\)\(mv^2\)
ゆえに、\(v\)=\(\sqrt{gl}\)です。
(2)については、鉛直方向とのなす角が一意に定まってないだけで、考え方は(1)と同じです。
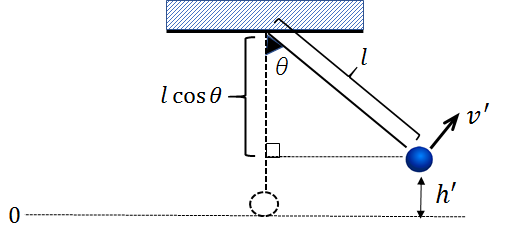
図において、おもりの基準点からの高さ(\(h'\))は、
\(l-lcosθ\)=\(l(1-cosθ)\)
よって、位置エネルギーは\(mgl(1-cosθ)\)です。
また、この地点におけるおもりの速さを\(v'\)とすると、運動エネルギーは\(\Large\frac{1}{2}\)\(mv'^2\)となります。
よって、この地点の力学的エネルギーは、
\(mgl(1-cosθ)\)+\(\Large\frac{1}{2}\)\(mv^2\)・・・・・⑤
です。
力学的エネルギー保存則より③=⑤なので、
\(\Large\frac{1}{2}\)\(mgl\)=\(mgl(1-cosθ)\)+\(\Large\frac{1}{2}\)\(mv^2\)
\(\Large\frac{1}{2}\)\(mv^2\)=\(-mgl\)+\(mglcosθ\)+\(\Large\frac{1}{2}\)\(mgl\)
=\(mglcosθ\)-\(\Large\frac{1}{2}\)\(mgl\)
\(v'^2\)=\(2glcosθ\)-\(gl\)
よって、\(v'\)=\(\sqrt{gl(2cosθ-1)}\)です。
試しに、この結果に\(θ\)=\(0°\)を代入してみましょう。
\(v'\)=\(\sqrt{gl(2cos0°-1)}\)
=\(\sqrt{gl(2×1-1)}\)
=\(\sqrt{gl}\)
\(θ\)が\(0°\)となるのは、おもりが最下点にある場合なので、(1)の結果と一致しましたね。
同じ要領で、鉛直方向とのなす角が\(30°\)や\(60°\)の時の速さを求めることができます。
なお、\(θ\)=\(60°\)を代入すると\(v'\)=\(0\)となりますが、これは単振り子において力学的エネルギーが保存される場合、おもりはスタート地点と同じ高さまで上がることを示しています。
今回、力学的エネルギー保存則を使って解いていきましたが、小球がコースターの上を運動する問題でも同じような解き方をしています。
このように運動の状況が違っても、基準点を決めて力学的エネルギー保存則を使える問題はいくつもありますので、繰り返し練習して慣れていってくださいね。