今回は、はたらく力を分解する状況を見ていきましょう。
下の図のように、水平面から角度\(θ\)だけ傾いた斜面上に質量\(m\)の物体が置かれているとき、物体には重力\(mg\)がはたらいています。

この\(mg\)を、「斜面方向」と「斜面に垂直な方向」に分解すると、次のようになります。
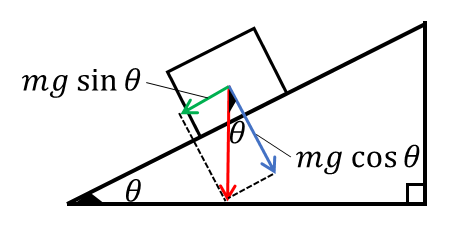
教科書や問題集で目にするお馴染みの形ですね。
ただし、斜面の角度の取り方が次のような場合は、\(sinθ\)と\(cosθ\)が逆になります。
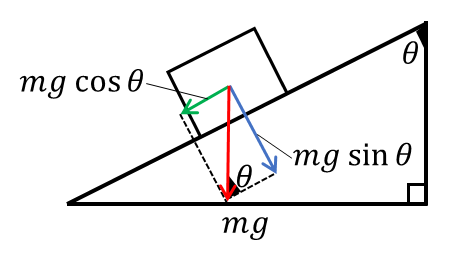
\(θ\)がこのように指定されるケースはあまり見かけませんが、「斜面方向がsin」という認識だと、イレギュラーな問題に引っかかる恐れがあるので注意してください。
--------------------------------------
別のケースとして、天井から垂れている糸に繋がれた物体が、斜面上で静止している場合を考えてみましょう。
糸は鉛直方向から\(θ\)だけ傾いています。
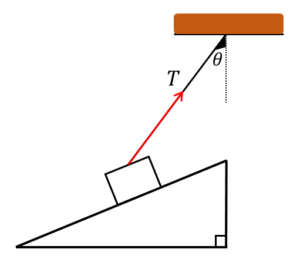
この場合、糸の張力\(T\)は、分解するとどのように表されるでしょうか?
何よりもまずは、「斜面方向」と「斜面に垂直な方向」の成分に分解することです。
そうすると、互いに相似な三角形が見つかります。
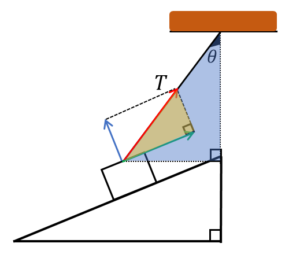
ゆえに、糸の天井からの傾き加減\(θ\)は、張力\(T\)のベクトルを含む三角形の一つの角と同じになります。
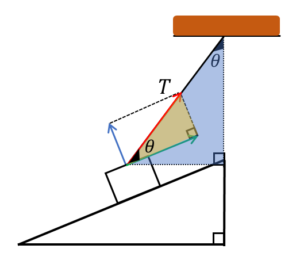
したがって、張力\(T\)の斜面方向の成分は\(Tcosθ\)、張力\(T\)の斜面に垂直な方向の成分は\(Tsinθ\)、と表すことができます。
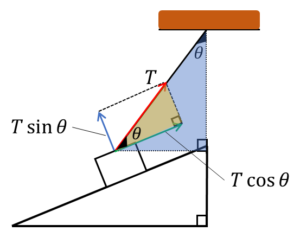
既に気づいた人もいると思いますが、この物体には糸の張力以外に、重力もはたらいています。
斜面上の物体にはたらく重力は冒頭のように分解できるので、力のつり合いを考えたい時は、張力も斜面方向に分解しなければいけません。
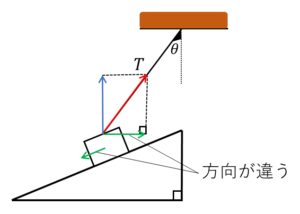
(上図のように分解すると、重力の斜面方向の成分と方向が違うので、つり合いの式が立てられません。)
基礎的な内容ですが、復習も兼ねて今一度頭の中に入れておいてください。