慣性系と非慣性系の違い

「慣性系」や「非慣性系」という言葉は、かの有名なアインシュタインが発表した「相対性理論」の取っ掛かりとしてとてもよく出てきます。

高校物理で直接は習いませんが、それぞれの意味と違いについて簡単にまとめてみたいと思います。

出発点は「座標」

まず初めに、中学で習った「座標」というものを思い出してみてください。

座標とは、簡単に言えばある点の位置を示すための数の組み合わせのことで、（1,2）とか（-1,-5）などと表されます。

このように点の位置を座標で表せるのは、原点とか、横軸がx軸だとかが、色々決まっているからで、このような取り決めのことを、座標系といいます。

座標系の例として、下図のようなものがあります。

数学で何度も出てきているので、馴染み深いのではないでしょうか。

この座標系は、原点をO、横軸をx軸、縦軸をy軸としており、なおかつx軸とy軸は直行しています。

このように「座標系」を決めることで、初めて任意の点を（1,2）などと表すことができます。

慣性系と非慣性系

さて簡単に座標系を説明したところで本題に入りますが、

「慣性系」とは、運動の第１法則と、運動の第２法則が成り立つ座標系のことです。

この運動の法則とは、それぞれ次のようなものです。

これらが成り立つ座標系があれば、逆に成り立たない座標系もあります。

成り立たない方の座標系を、非慣性系といいます。

慣性系と非慣性系の具体例

下図のように、Ａさんは地上に立っており、Ｂさんは加速度\(a[m/s^2]\)で水平右向きに動く電車の中に乗っているとします。

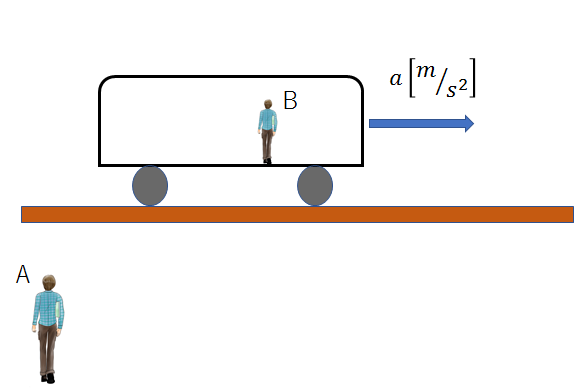
この場合、ＡさんとＢさんでは、見える世界(景色)が違います。

Ａさんは周囲の山や建物は止まって見え、電車は右向きに動いているように見えます。

一方Ｂさんは、電車と共に動いているので、Ａさんも周囲の景色も動いて見えます。

このように、二人は見える景色が違うので、同じ世界として考えるとややこしくなります。

そこで、ＡさんとＢさんとで、それぞれ違う座標系を考えます。

-------------------------------------------

つまり、水平方向右向きを正として、

Ａさんがいる世界の座標系（\(S\)）と、Ｂさんがいる世界の座標系（\(S'\)）を定義し、別の世界として考えるということです。

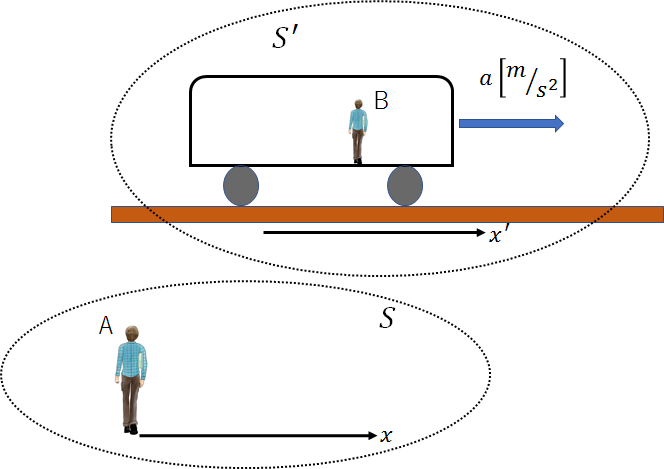
（厳密にはＡさんとＢさんは当然、同じ世界（地球上）にいるのですが、物理学的に考える場合、二人の動き(運動の状態)が違うので、互いに別物として扱います）

-------------------------------------------

ここまで、ＡさんとＢさんそれぞれの座標系を定義しましたが、この二つは慣性系でしょうか？非慣性系でしょうか？

ポイントとなるのは、周囲の景色の「見え方」です。

静止しているＡさんの立場から電車を見ると、電車全体が右向きに加速しているように見えます。

実際、電車は右向きの力によって右向きに加速しているので、運動方程式\(ma\)＝\(F\)が成り立ち、Ａさんの見え方と矛盾しません。

このことから、Ａさんの座標系\(S\)は、「慣性系」です。

問題は、Ｂさんからの見え方です。

電車が加速しているので、Ｂさんから見たＡさんは、電車と真逆の向きに加速しているように見えます。

しかし、実際はＡさんは静止したままです。何も外力を受けていないので、運動の第１法則により、加速はしていません。

つまり、実際のＡさんの運動の状態と、Ｂさんから見たＡさんの運動の状態が矛盾しています。

これはすなわち、Ｂさんから見た世界は、運動の第１法則も第２法則も成り立っていません。

なので、Ｂさんの座標系\(S'\)は、「非慣性系」です。

電車が加速していない場合は？

上記の例で、もしもＢさんが乗っている電車が等速度で右向きに動いている場合はどうでしょうか？

Ａさんからは、Ｂさんや電車が等速度で右向きに運動しているように見えます。

逆にＢさんからも、Ａさんが等速度で電車と逆向きに運動しているように見えます。

Ｂさんから見たＡさんの状態は、外力を受けていないＡさんの振る舞い（静止もしくは等速度運動）と矛盾しておらず、運動の第１法則、第２法則ともに成り立ちます。

よって、この場合、ＡさんとＢさんの座標系はともに慣性系となります。

-------------------------------------------

このように、加速しているかしていないかによって、周囲の見え方も違ってきます。

それにより、座標系も慣性系であったり非慣性系であったりするので、注意してください。