水の中に入ると、地上よりも体が軽くなった感じがしますよね。
これはまさに、水中では体を浮き上がらせようとする力、すなわち「浮力」がはたらいているからです。
今回は、主に液体に物を入れた時に関係する、浮力について紹介したいと思います。
-----------------------------
一般的に、水中に入れた物体には、その物体に垂直な方向にあらゆる力がはたらきます。

浮力とは、これらの力のうち、物体の下面にはたらく力\(F_2\)から、物体の上面にはたらく力\(F_1\)を引いたものです。
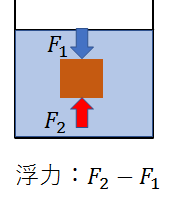
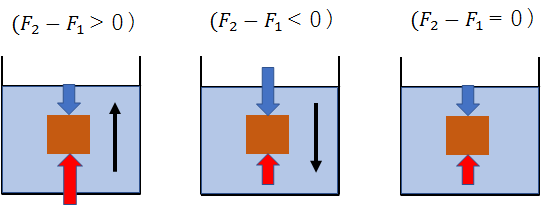
\(F_2-F_1>0\)、すなわち下面にはたらく力の方が大きいと、物体は浮き上がります。
\(F_2-F_1<0\)、すなわち上面にはたらく力の方が大きいと、物体は沈んでいきます。
\(F_2-F_1=0\)、すなわち上面にはたらく力と下面にはたらく力が等しいと、物体は静止します。
浮力を求める一般式は?
繰り返しになりますが、物体にはたらく浮力は、「物体の下面にはたらく力」から「物体の上面にはたらく力」を引くと求められます。
さらに具体例を挙げて、浮力の一般的な式を求めてみましょう。
-----------------------------
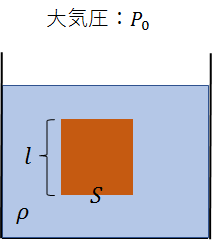
下の図のように、底面積\(S[m^2]\)、高さ\(l[m]\)の直方体を、容器に入っている密度\(ρ[kg/m^3]\)の液体の中に入れたとします。
なお、大気圧は\(P_o\)とします。
物体が液体の中に入った瞬間から、物体には力がはたらきます。
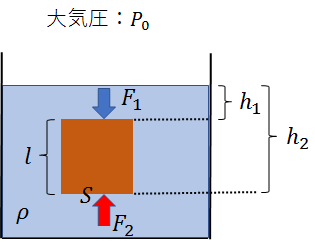
ここで、水面からの深さ\(h_1\)の地点で物体の上面にはたらく力を\(F_1\)、水面からの深さ\(h_2\)の地点で物体の下面にはたらく力を\(F_2\)とします。
圧力の公式より、「圧力=面を垂直に押す力÷力が働く部分の面積」なので、
変形させると、「面を垂直に押す力=圧力×力が働く部分の面積」となります。
今回、力が働く部分の面積は上面も下面も\(S[m^2]\)なので、この式に当てはめると、
\(F_1\)=深さ\(h_1\)の地点の圧力×\(S\)・・・①
\(F_2\)=深さ\(h_2\)の地点の圧力×\(S\)・・・②
となります。
さらに、深さ\(h_1\)、\(h_2\)それぞれの地点の圧力をそれぞれ\(P_1\)、\(P_2\)とすると、
液体中の圧力を求める式より、\(P_1=P_o+ρh_1g\)、\(P_2=P_o+ρh_2g\)(Poは大気圧)なので、
これらを①と②にそれぞれ代入して、
\(F_1\)=\((P_o+ρh_1g)×S\)・・・③
\(F_2\)=\((P_o+ρh_2g)×S\)・・・④
これで、まずは物体の上面と下面それぞれにはたらく力を式で表すことができました。
-----------------------------
さあ、もう少しです。
浮力とは、物体の下面にはたらく力(F2)から、物体の上面にはたらく力(F1)を引いたものなので、
④-③より、
\(F_2-F_1\)
=\((P_o+ρh_2g)×S-(P_o+ρh_1g)×S\)
=\(ρh_2g×S-ρh_1g×S\)
=\(ρ(h_2-h_1)g×S\)
ここで、\(h_2-h_1\)は直方体の高さ\(l\)と同じなので、\((h_2-h_1)×S\)は、直方体の体積を表すことになります(底面積×高さだから)。
よって、体積を\(V[m^3]\)とおくと、最終的に\(F_2-F_1\)=\(ρVg\)となり、これが直方体にはたらく浮力となります。
\(ρ\):流体の密度、\(V\):物体の体積、\(g\):重力加速度
この式には、深さを表すものが含まれていません。
浮力は、物体がどの深さにいようが、どこでも同じなのです。
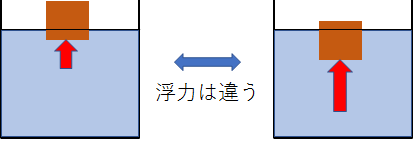
ただしこれは、物体が完全に水中に浸かっている場合に限ります。
下図のように物体の一部が空気中に出ている状態だと、その位置によって浮力は違います。
なお、浮力と関連が深いものとして「アルキメデスの原理」があります(別記事にて紹介しています)。