本項では、加速度が絡む問題を解くうえで欠かせない、3つの公式についてご紹介します。
等加速度直線運動とは?
物体の運動の中でも特に加速度が一定の運動を「等加速度運動」と言いますが、このうち直線上を運動している場合を、「等加速度直線運動」と言います。
ややこしいですが、等加速度運動と等加速度直線運動は、必ずしもイコールではありません。
例えば物体を斜め上方に投げる場合、加速度が一定なので等加速度運動ですが、物体の軌道が放物線を描くため、直線運動ではないからです。
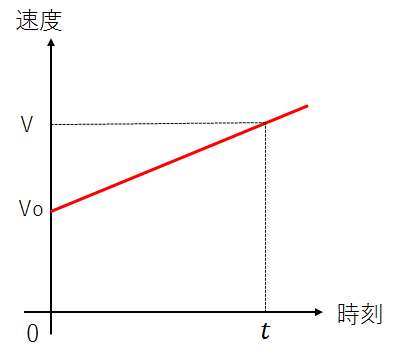
これから紹介する公式は、特に等加速度直線運動とみなされる場合に使用するものですので、間違えないようにしてください。 ある物体が、直線上を一定の加速度\(a[m/s^2]\)で運動しているとします。 観測を始めた瞬間の時刻を\(t=0\)[s]とし、その時点における物体の速度を\(v_o\)とします。 そこから時間が経って時刻\(t\)[s]になった時の速度と変位をそれぞれ\(v\)、\(x\)とすると、下記の式が成り立ちます。 $$v=v_o+at$$ $$x=v_ot+\frac{1}{2}at^2$$ $$v^2-v_o^2=2ax$$ 今後、時間が限られている中で様々な問題を解く際は、おそらく公式を無意識にそのまま使わざるを得ないかと思います。 もちろんそのまま覚えてしまっても良いのですが、なぜこのような形になるかは以下に順番に示してありますので、一度だけでも目を通しておいてくださいね。 ある時刻(\(t=0\)[s])の物体の速度が\(v_0\)[m/s]の時、そこから\(t\)[s]後の物体の速度(=\(v\)[m/s])は果たしてどのくらいになっているでしょうか? 加速度が生じているとは?でもお話しましたが、加速度は速度の変化量を時刻の変化量で割ると、求めることができます。 今、時刻0[s]から\(t\)[s]までの間に、物体の速度が\(v_0\)[m/s]から\(v\)[m/s]へ変化しているとします。 つまり、速度の変化量は\(v-v_0\)[m/s]、時刻の変化量は\(t-0\)[s]なので、この場合の加速度\(a[m/s^2]\)は、 $$a=\frac{v-v_0}{t-0}=\frac{v-v_0}{t}$$ となります。 これを変形すると、 $$at=v-v_0$$ $$∴ v=v_0+at・・・・・(1)$$ つまり、\(t\)秒後の物体の速度\(v\)は、初めの速度(=初速度)に、物体の加速度とかかった時間の積を加えて求めることができます。 上記の運動を、縦軸に速度、横軸に時刻をとってグラフに表すと、下記の図のようになります。 加速度が一定なので、物体の速度は一定の割合で増えていきます。よって、グラフは右上がりの直線です。 また、t=0の時点で元々物体には速度\(v_0\)がありましたから、t=0における値は\(v_0\)です。 ここで、有名な「距離=速さ×時間」の公式から、物体の変位を求めてみます。 今回、物体は一直線上を運動しているので、進んだ距離=変位と言えます。 すなわち物体が進んだトータルの距離は、上記のグラフで見ると、直線と、横軸、縦軸で囲まれる部分の面積になりますので、台形の面積の公式((上底+下底)×高さ×\(\frac{1}{2}\))を使うと、物体の変位\(x\)[m]は、 $$x=(v_0+v)*t*\frac{1}{2}$$ この式の\(v\)に(1)を代入すると、 $$x=(v_0+v_0+at)*t*\frac{1}{2}$$ $$=v_0t+\frac{1}{2}at^2・・・(2)$$ となります。 問題文中に時刻\(t\)が与えられていない場合は、上記で求めた式(1)、(2)から\(t\)を消去すれば、新たな式を作ることができます。 (1)より、\(t=\large\frac{v-v_0}{a}\) これを(2)に代入すると、 $$x=v_0(\frac{v-v_0}{a})+\frac{a}{2}*(\frac{v-v_0}{a})^2$$ \(\large∴ v^2-v_0^2=2ax\) となります。 今回取り上げた公式は、様々な物体の運動、特に「自由落下」「鉛直投げおろし」「鉛直投げ上げ」「水平投射」「斜方投射」を解くために、とてもよく使います。 なるべく必要な時にすぐ浮かぶよう、頭の中に入れておいてくださいね。
公式その1~速度の式~
公式その2~変位の式~
$$=(2v_0+at)*\frac{t}{2}$$公式その3~時刻tを含まない式~
$$=\frac{v_0v-v_0^2}{a}+\frac{a}{2}*\frac{v^2-2v_0v+v_0^2}{a^2}$$
$$=\frac{v_0v-v_0^2}{a}+\frac{v^2-2v_0v+v_0^2}{2a}$$
$$=\frac{2v_0v-2v_0^2+v^2-2v_0v+v_0^2}{2a}$$
$$=\frac{v^2-v_0^2}{2a}$$物体の運動のベースとなる