物体を斜めに引っ張る
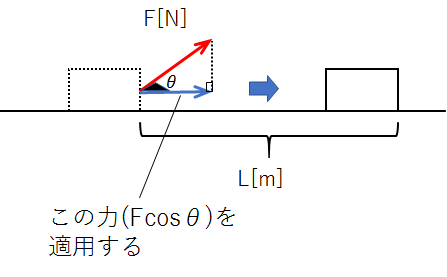
図より、加えた力\(F\)の水平成分は\(Fcosθ\)です。
これで、加えた力の向きと物体の移動した向きが同じになりました。
よって、加えた力がした仕事は、\(Fcosθ×L\)です。
張力がする仕事(単振り子)
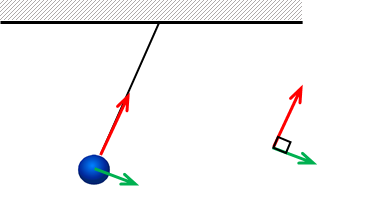
図のような単振り子では、張力\(T\)の向きと先端に付けたおもりが移動する向きは、常に直角(=90°)になります。
ゆえに、仕事を求める式の\(cosθ\)はゼロであることから、張力がおもりにした仕事も「ゼロ」です。
張力はおもりの運動に全く関与しないことがわかります。
(振り子が左右に振れるのは、振り子にはたらく重力の影響です)
摩擦力がする仕事
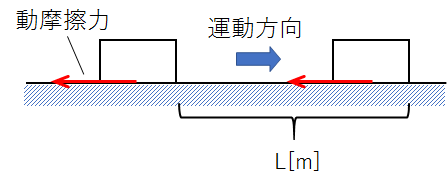
あらい水平面に置かれた物体が運動している時、物体にはたらいている摩擦力は動摩擦力でした。
動摩擦力は運動を妨げる向きにはたらくため、力の方向は物体の移動方向と逆向きです。
よって、摩擦力がした仕事は、動摩擦係数を\(μ'\)とすると、
\(μ'mgcos180°×L\)
=\(-μ'mgL\)
です。
手が小球にする仕事
質量\(m\)の小球を手にのせてゆっくり上げ下げする場合、手が小球にした仕事はどうなるでしょうか。
これは、上げる場合と下げる場合で違います。
●上げる場合
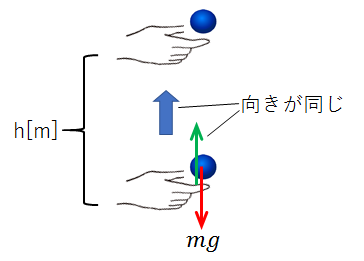
小球には、鉛直下向きに重力\(mg\)がかかっています。
ですので、小球を高さ\(h\)[m]まで上げる最中、手が小球にかけている力(緑ベクトル)は上向きに\(mg\)です。
この力は小球の移動方向と同じなので、手が小球にした仕事は、\(mgh\)です。
●下げる場合
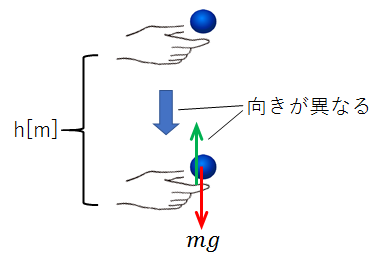
小球には、鉛直下向きに重力\(mg\)がかかっています。
ですので、小球をある高さから\(h\)[m]だけ下げている最中、手が小球にかけている力は上向きに\(mg\)です。
注意すべきは、この場合小球は下がっているので、手の力の向きは小球の移動方向と真逆です。
よって、手が小球にした仕事は、\(-mgh\)(\(mgcos180°×h\))です。