位置エネルギーを求める際の基準点は、どこでも好きなところにとって良いですが、とる場所によって、位置エネルギーの値は変わってきます。
今回は仕事とエネルギーの観点から、重力と万有引力それぞれの力による位置エネルギーを求めてみました。
重力による位置エネルギー
質量\(m\)の物体が地上から高さ\(h\)の地点にある時、地上を基準点とすると、この物体は位置エネルギー\(mgh\)をもっています。

これは言い換えれば、物体は地上から高さ\(h\)の地点まで持ち上げられたことで、エネルギー(=位置エネルギー)を蓄えたということです。
持ち上げられたということは、外部から仕事をされたことと同じです。
一般に、ある力を加えて物体を移動させた時、物体がされた仕事は、その力と移動区間で囲まれた面積部分になります。
今回、物体を移動させるためには上向きに\(mg\)の力を加えなければいけないので、物体がされた仕事は下図の青色部分になり、これは\(mg\)という力を、0から\(h\)まで積分することで求められます。
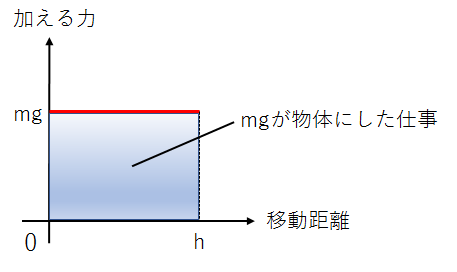
実際に積分の式に当てはめてみると、
\(\Large\int_0^h\)\(mgdx\)=\([mgx]^h_0\)=\(mgh\)
となって、確かに「高さ\(h\)の地点の物体の位置エネルギー」と一致しています。
-------------------------------
今度は逆に、高さ\(h\)の地点を基準とし、高さ0(地上)の地点の位置エネルギーを積分によって求めてみましょう。
この場合、高さ\(h\)の地点が基準なので0、高さ0(地上)の地点が\(-h\)となることに注意してください。
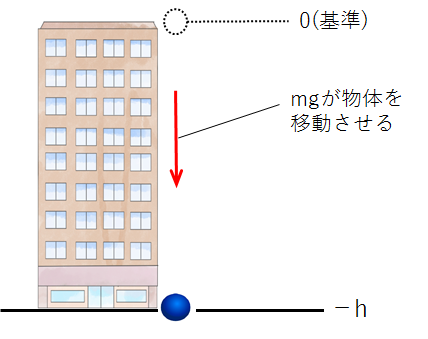
物体に蓄えられた位置エネルギーは、「基準から\(-h\)の地点まで重力\(mg\)が物体にした仕事」になります。
つまり、重力\(mg\)という力を0から\(-h\)まで積分したことと同じなので、位置エネルギーは、
\(\Large\int_0^{-h}\)\(mgdx\)=\([mgx]^{-h}_0\)=\(-mgh\)
となります。
基準から\(h\)だけ下がっているので、位置エネルギーは負の値です。
万有引力による位置エネルギー
万有引力による位置エネルギーの場合も基準点はどこにとっても良いですが、一番楽なのは無限遠にとることです。
(理由はこちらで説明しています。)
ここで、地球の中心からの距離を\(r\)とし、\(r\)=\(R\)における物体の位置エネルギーを求めてみましょう。
重力の場合と同じように、位置エネルギーは基準となる無限遠(\(r\)=\(∞\))から\(r\)=\(R\)の地点までの間、物体にはたらく力(万有引力)がする仕事になります。
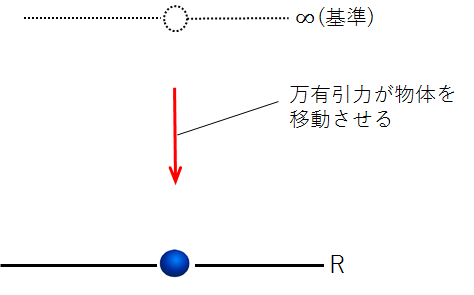
万有引力は地球と物体の質量をそれぞれ\(M\)、\(m\)、万有引力定数を\(G\)とすると\(\frac{GMm}{r^2}\)と表されますので、実際に積分の式に当てはめてみると、
\(\Large\int_∞^R\)\(\frac{GMm}{r^2}dr\)=\([-\frac{GMm}{r}]^R_∞\)=\(-\frac{GMm}{R}\)
となります。
これは、地球の半径を\(R\)とした場合の、地球表面における位置エネルギーのことです。
万有引力による位置エネルギーは少し特殊で、基準より手前側にもかかわらず、常に負の値となることを覚えておいてください。