密度とは、その物体の単位体積あたりの質量(kg)をいいます。
「単位体積あたり」とは「1\(m^3\)あたり」のことなので、密度の単位は[kg/\(m^3\)]です。
言い換えれば、物体1\(m^3\)の質量が何kgか?ということを表しています。
例えば、ある物体Aと物体Bがあり、物体Aの方が1\(m^3\)あたりの質量が大きい場合、「物体Aの方が物体Bよりも密度が大きい」ことになります。
ちなみに、水の密度は1000[kg/\(m^3\)]です。
1\(m^3\)あたりの質量は何と1000[kg](軽自動車とほぼ同じ)です。結構重いんですね。
なお、物理では密度の量記号として\(ρ\)(ロー)を使うことが多いので、覚えておいて下さい。
水の底面の圧力は?
ここで、図のような体積が1㎥の水の底面にかかる圧力を考えてみましょう。

圧力を求める式として、下記の公式があったのを覚えているでしょうか?
前述したように1\(m^2\)の水の質量は1000[kg]なので、底面にはたらく力は、重力加速度を\(g\)とすると1000×\(g\)となります。
一方、力が働く部分、すなわち底面の面積は、1[m]×1[m]=1[\(m^2\)]です。
よって、求める圧力は、
(1000×\(g\))÷1=1000×\(g\)
となります。
----------------------------
では、同じ1㎥でも下図のような場合はどうでしょう?
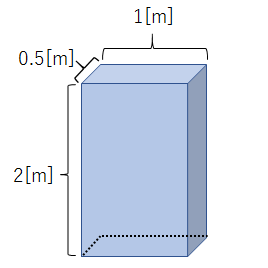
底面にはたらく力は先程と同じで1000×\(g\)[N]ですが、底面の面積は、0.5[m]×1[m]=0.5[\(m^2\)]となります。
よって、求める圧力は、
(1000×\(g\))÷0.5==2000×\(g\)
です。
----------------------------
さらに、次のような場合はどうでしょう?
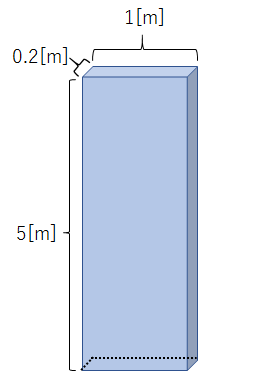
底面にはたらく力はこれまでと変わらず1000×\(g\)[N]ですが、底面の面積は、0.2[m]×1[m]=0.2[\(m^2\)]となります。
よって、求める圧力は、
(1000×\(g\))÷0.2==5000×\(g\)
です。
以上をまとめると、次のようになります。
深さ1[m]の底面の圧力・・・1000×\(g\)
深さ2[m]の底面の圧力・・・2000×\(g\)(=2×1000×\(g\))
深さ5[m]の底面の圧力・・・5000×\(g\)(=5×1000×\(g\))
この結果から、深さが元の2倍になると圧力も2倍となり、さらに元の5倍になると圧力も5倍となることがわかります。
圧力は、深さによって変わってくるのです。
一般的な表し方
重力加速度を\(g\)、流体(液体及び気体のこと。ここでは水)の密度を\(ρ\)とすると、水面からの深さ\(h\)[m]の地点の圧力\(P\)[Pa]は、下記の式で表すことができます。
前に求めた深さ2[m]の底面の圧力(2×1000×\(g\))の場合、\(h\)=2、\(ρ\)=1000ということです。
注意すべきは、1000の部分は水の質量ではなく、水の密度という点です。
質量じゃないの?と思ったかもしれませんが、これは水の密度が1000[kg/㎥]なので質量も1000[kg]となり、たまたま同じ数値になっただけです。
間違えやすいので注意してください。
なお、圧力の式は順序を入れ替えて\(ρhg\)としている参考書が結構あります。
容器に入った水の場合
これまでの例では単に水のかたまりを扱いましたが、基本的に色々な問題では容器に入った水を扱うことが多く、容器の上面は、大抵空気にさらされています。
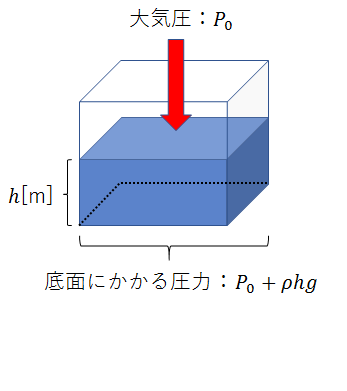
この場合は、空気の圧力(大気圧)も考える必要があり、圧力の式は、\(P\)=\(Po\)+\(hρg\)となります。