円運動の問題では、単振り子や円錐振り子のように、天井から吊るされた糸に小球が付いているケースをよく見かけますよね。
ですが、他にも面白いシチュエーションがあります。
例えば下図のように、穴のあいた小球が輪に通されており、輪に沿って滑らかに動くことができるような場合です。

輪が動かない状態だと小球も最下部で静止していますが、
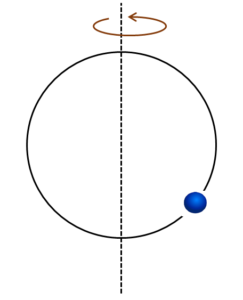
輪が、その中心を通る鉛直軸の回りに回転すると、小球はその影響を受けて少し離れた位置で静止します。
この時、小球にはどのような力がはたらいているでしょうか?
---------------------------------
仮に輪の半径を\(r\)、回転時の角速度を\(ω\)、小球の質量を\(m\)、重力加速度を\(g\)とします。
まず何といっても、重力\(mg\)ですね。
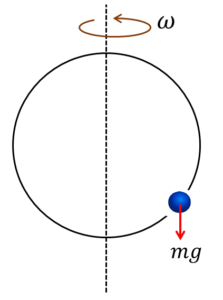
重力は、この世に存在する全ての物に対してはたらくのでした。
次に、小球も輪とともに回転しているので、それに伴う力を考慮しなければなりません。
これは向心力と遠心力の違いでも紹介していますが、輪の回転をどこから見るかによって違います。
→向心力(円運動をしている物体にはたらく中心方向の力)
●輪と一緒に回転している位置から見る場合
→遠心力(向心力と大きさが同じ逆向きの力)
今回は小球に乗って一緒に回転しているとしましょう。
そうすると、はたらく力は「遠心力」ですね。
一般に、遠心力は円運動する物体の質量と円運動の半径、角速度を用いて表され、向きは中心方向(向心力の方向)と逆向きです。
鉛直軸と輪の半径がなす角を\(θ\)とすると、\(mrω^2\sinθ\)となります。
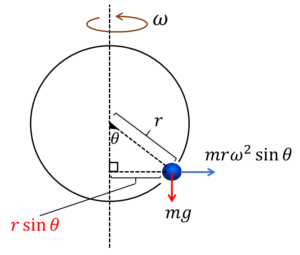
用いる半径が\(r\)ではないことに注意してください。
小球にはたらく遠心力は、小球から見て回転軸に垂直な向きの半径を採用します。
さて、これで小球にはたらく力は全部でしょうか?
実はあとひとつ、小球と輪が接しているので、輪からの垂直抗力がはたらいています(仮に\(N\)とおいています)。
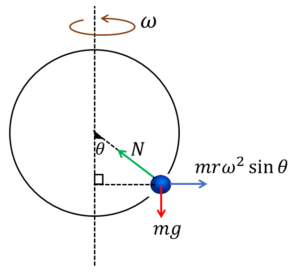
一番忘れやすいので要注意です。
---------------------------------
今回小球にはたらく力を書き入れた図は、向心力と遠心力をうまく使い分けて立式しようの図とほぼ同じですよね。
つまり、小球が糸に繋がれていようが、輪に通されていようが、円運動をしていれば似たような力がはたらくということです。
入試問題レベルになると複雑な運動もありますが、まずは対象の物体にはたらく力をひとつずつ洗い出すことが、正答への第一歩です。