単振り子とは、質量が無視できる糸の一端を固定し、他端に質点とみなせるおもりをつけた振り子のうち、おもりが鉛直面内で円弧または円周を描いて動くものを指します。

すなわち、おもりは円の中心を固定点とした円運動をすると言えます。
今回は、この単振り子の力のつり合い式についてまとめてみました。
単振り子にはたらく力は?
先端のおもりの質量を\(m\)、重力加速度を\(g\)とすると、おもりにはたらいている力は下図のとおりです。
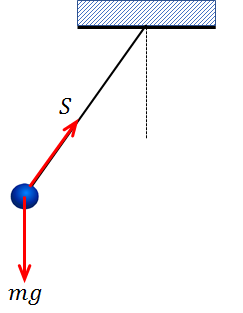
なお、\(S\)は糸の張力で、円の中心に向かう力です。
円運動をしている物体には、必ずこの中心に向かう力がはたらいており、この力を向心力といいます。
おもりの運動の状態に注目
単振り子の場合、糸が伸びたり縮んだりしないとすると、おもりは糸の張力方向には運動しません。
よって、糸の張力方向について力のつり合い式が立てられます。
(色々なところで書いていますが、物体にはたらく力がつり合っているのは、その物体が静止している時か、等速直線運動をしている時です。)
糸が円直線となす角を\(θ\)とすると、重力\(mg\)の張力方向の成分は\(mgcosθ\)となります。
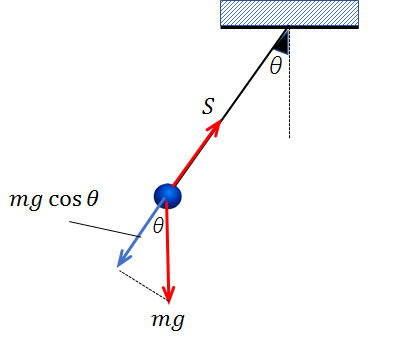
よって、力のつり合い式は、
\(S\)=\(mgcosθ\)
となります。
-----------------------------
ちなみに、水平方向と鉛直方向については力のつり合いの条件を満たしていない(静止したり等速直線運動をしていない)ため、つり合い式は立てることができません。
別項で円錐振り子の力のつり合い式についてもお話していますが、どちらの振り子も、このような条件を満たす方向のつり合い式を立てることがポイントです。