人工衛星を無限遠に飛ばすためには？

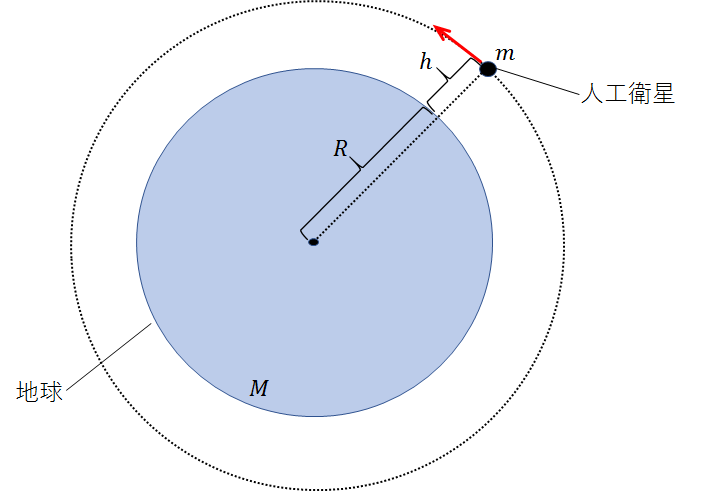
運動中の人工衛星が、二度と戻ってこないようにするために与えるエネルギーはいくらか？という問題です。

人工衛星の力学的エネルギーを求めてみる

まずは、運動している最中の人工衛星の力学的エネルギーを求めます。

＜運動エネルギー＞

人工衛星の速度を\(v\)とすると、人工衛星に生じる加速度は地球の中心向きに\(\frac{v^2}{R＋h}\)、人工衛星にはたらく力は、地球と人工衛星との間の万有引力(同じく地球の中心向き)\(\frac{GMm}{(R＋h)^2}\)なので、

人工衛星の運動方程式は、

\(m\Large\frac{v^2}{R＋h}\)＝\(\Large\frac{GMm}{(R＋h)^2}\)

となります。

この式より\(v\)＝\(\sqrt\frac{GM}{R＋h}\)なので、運動エネルギーは、

\(\Large\frac{1}{2}\)\(mv^2\)＝\(\Large\frac{GMm}{2(R＋h)}\)

です。

＜位置エネルギー＞

地球の中心から\(r\)だけ離れた地点の万有引力による位置エネルギーは、無限遠を基準として\(－\frac{GMm}{r}\)と表されるので、\(r\)にそのまま\(R＋h\)を代入して、

\(－\Large\frac{GMm}{R＋h}\)

です。

---------------------------------

以上より、人工衛星の力学的エネルギー(運動エネルギー＋位置エネルギー)は、

\(\Large\frac{GMm}{2(R＋h)}\)\(－\Large\frac{GMm}{R＋h}\)・・・・・①

となります。

無限遠における人工衛星の力学的エネルギーは？

①式を求めたように、一般的に任意の点\(r\)を速度\(v\)で運動している物体の力学的エネルギーは、次のように表されます。

\(\Large\frac{1}{2}\)\(m{v}^2\)\(－\Large\frac{GMm}{r}\)・・・・・②

仮に人工衛星が無限遠に行ったと仮定し、その時の速度を\(v'\)とします。

無限遠では\(r\)＝\(∞\)なので、②式において\(－\frac{GMm}{r}\)はゼロとなります。

よって、無限遠における人工衛星の力学的エネルギーは、

\(\Large\frac{1}{2}\)\(m{v'}^2\)・・・・・③

です。

力学的エネルギー保存則を適用

万有引力は保存力なので、力学的エネルギー保存則が成り立ちます。

つまり、人工衛星にエネルギー\(E\)を加えた状態の力学的エネルギーと、無限遠に到達した状態の力学的エネルギーは、等しいということです。

よって、

\(\Large\frac{GMm}{2(R＋h)}\)\(－\Large\frac{GMm}{R＋h}\)＋\(E\)＝\(\Large\frac{1}{2}\)\(m{v'}^2\)・・・④

ここで、人工衛星が無限遠の地点でまだ速度をもっていれば(\(v'\)≧0であれば)、人工衛星は無限遠に到達しているといえます。

よって、\(v'\)≧0のとき「(④式の右辺)≧0」なので、同時に④式の左辺も0以上ということになり、

\(\Large\frac{GMm}{2(R＋h)}\)\(－\Large\frac{GMm}{R＋h}\)＋\(E\)≧0

∴ \(E\)≧\(\Large\frac{GMm}{2(R＋h)}\)

この条件であれば、人工衛星は無限遠に到達するので、求める値は最小値である\(\Large\frac{GMm}{2(R＋h)}\)です。