図のように、水平面から\(θ\)だけ傾いたあらい斜面上に質量\(m\)の物体Aが置かれており、物体Aに結んだ糸の片端には、なめらかな滑車を通して質量\(M\)の物体Bがつるされている。
物体Aと斜面との間の静止摩擦力係数を\(μ\)、動摩擦係数を\(μ'\)、重力加速度の大きさを\(g\)として、以下の問いに答えよ。
ただし、\(tanθ\)>\(μ\)とする。

(1)\(M<M_1\)の時、物体Aは斜面を下方に滑る。\(M_1\)を\(m\)、\(μ\)、\(θ\)を用いて表せ。
(2)\(M>M_2\)の時、物体Aは斜面を上方に滑る。\(M_2\)を\(m\)、\(μ\)、\(θ\)を用いて表せ。
(3)物体Bのかわりに、質量\(M_3\)(>\(M_2\))の物体Cをつるしたところ、物体Aは一定の加速度で斜面を上方に滑った。
この時の加速度の大きさ\(a\)を\(m\)、\(M_3\)、\(g\)、\(μ'\)、\(θ\)を用いて表せ。
二つの物体は糸でつながれていますから、例えば片方の物体がとても重くなると、その物体に引っ張られてもう片方も移動してします。
片方の物体が静止していれば、もう片方も静止しています。
この問題の趣旨は、物体Bの質量によって、物体Aが移動する向きが変わるよ、というものです。
-----------------------------
(1) 仮に、物体Bの質量(\(M\))が\(M_1\)だとします。
物体Aが斜面を下方に滑りだすのは\(M<M_1\)の時なので、\(M=M_1\)である今は、物体AもBも静止したままです。
滑り降りる方向に移動しないよう、物体Aは頑張っていると考えると、物体Aにはたらく摩擦力\(f\)は、斜面を昇る向きです。
さらに言うと、物体Aは持ちこたえられる限界ぎりぎりの状態です。
ここから少しでも物体Bの質量が小さくなると、斜面方向の力\(mgsinθ\)によって、物体Aは滑り降りていきます。
よって、摩擦力は最大静止摩擦力となります。
これを\(f_0\)とおき、各物体にはたらく力を図示すると次のようになります。

\(N\)は物体Aが斜面から受ける垂直抗力です。
静止しているので各物体にはたらく力はつり合っていますから、それぞれの物体の力のつり合い式は、
物体A:\(T+f_0\)=\(mgsinθ\)
物体B:\(T\)=\(M_1g\)
この2式より、
\(M_1g+f_0\)=\(mgsinθ\)
なお、最大静止摩擦力は、静止摩擦係数と垂直抗力の積で表されるので、鉛直方向の力のつり合い式(\(N\)=\(mgcosθ\))も利用すると、
\(M_1g+μmgcosθ\)=\(mgsinθ\)
\(M_1g\)=\(mgsinθ-μmgcosθ\)
=\(mg(sinθ-μcosθ)\)
∴ \(M_1\)=\(m(sinθ-μcosθ)\)
物体Bがこの質量より少しでも小さくなると、物体Aは斜面を滑り降ります。
(2) 考え方は(1)と同じです。
物体にはたらく摩擦力の向きに注意してください。
この場合も、物体Bの質量(\(M\))が\(M_2\)だとしましょう。
物体Aが斜面を上方に滑りだすのは\(M>M_2\)の時なので、\(M=M_2\)である今は、物体AもBも静止したままです。
滑り上がる方向に移動しないよう、物体Aは頑張っていると考えると、物体Aにはたらく摩擦力\(f\)は、斜面を下る向きです。
この場合も、物体Aは持ちこたえられる限界ぎりぎりの状態です。
ここから少しでも物体Bの質量が大きくなると、斜面方向の力\(T\)によって、物体Aは滑り上がっていきます。
よって、この時も摩擦力は最大静止摩擦力となります。
これをまた\(f_0\)とおき、各物体にはたらく力を図示すると次のようになります。
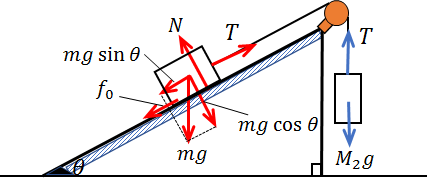
それぞれの物体の力のつり合い式は、
物体A:\(T\)=\(mgsinθ+f_0\)
物体B:\(T\)=\(M_2g\)
この2式より、
\(M_2g\)=\(mgsinθ+f_0\)
最大静止摩擦力を(1)と同様に表して\(f_0\)に代入すると、
\(M_2g\)=\(mgsinθ+μmgcosθ\)
=\(mg(sinθ+μcosθ)\)
∴ \(M_2\)=\(m(sinθ+μcosθ)\)
物体Bがこの質量より少しでも大きくなると、物体Aは斜面を滑り上がります。
(3) 物体AとCは糸でつながれているので、これらのの加速度の大きさは同じです。
今回は物体が運動している最中なので、斜面方向の力のつりあい式は使えません。
代わりに運動方程式を利用することになります。
また、物体Aにはたらく摩擦力も、この場合は静止摩擦力ではなく動摩擦力であることに注意してください。
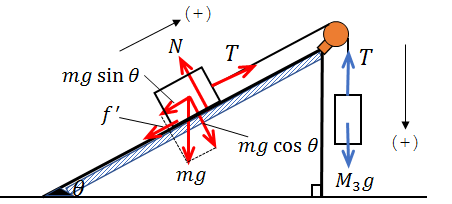
物体AとCの加速度を\(a\)、物体Aにはたらく動摩擦力を\(f'\)とおくと、それぞれの物体の運動方程式は、
物体A:\(ma\)=\(T-mgsinθ-f'\)
物体C:\(M_3a\)=\(M_3g-T\)
(物体Aは斜面を上方に滑るので、この向きを正、物体Cは降下するので、鉛直下向きを正としました。)
左辺同士、右辺同士をそれぞれ足し合わせて\(T\)を消去すると、
\((m+M_3)a\)=\(M_3g-mgsinθ-f'\)
動摩擦力は、動摩擦係数と垂直抗力の積で表されるので、鉛直方向の力のつり合い式も利用すると、
\((m+M_3)a\)=\(M_3g-mgsinθ-μ'mgcosθ\)
∴ \(a\)=\(\Large\frac{M_3g-mgsinθ-μ'mgcosθ}{m+M_3}\)
=\(\Large\frac{M_3-m(sinθ-μ'cosθ)}{m+M_3}g\)
-----------------------------
以上のように、物体同士が糸でつながれていると、片方の物体の質量によって、もう片方の物体にかかる力の向きも変わります。
まずは、物体が動こうとしている向きに注意して、式を立てるようにしてみてください。