図のように、長さが\(l\)の軽い糸の一端を点Oに固定し、他端に質量\(m\)の小球を取り付けた。
この小球を、糸がたるまないよう点Oと同じ高さの点Aまで持ち上げて静かに離したところ、小球は最下点Bを通過後、点Bから\(r\)だけ離れた真上の地点Cに打たれた釘を中心とする円運動を行った。

重力加速度を\(g\)として、以下の問いに答えよ。
(1)点Bに達した瞬間の小球の速さ\(v_B\)を求めよ。
(2)点Cから\(r\)だけ離れた真上の地点Dにおける小球の速さを求めよ。
(3)糸がたるむことなく点Dを通過するための、点Bと点Cの最大距離\(r_m\)を求めよ。
(1) 小球には重力と糸の張力がはたらいていますが、糸の張力は小球の進行方向と常に垂直なので、小球に対して仕事をしません。
よって、点Aと点Bそれぞれにおける力学的エネルギーの総和は等しくなります。
今回、最下点Bを位置エネルギーの基準とすると、
点Aの力学的エネルギーは\(mgl\)+\(0\)=\(mgl\)、
点Bの力学的エネルギーは\(0\)+\(\Large\frac{1}{2}\)\(mv^2_B\)=\(\Large\frac{1}{2}\)\(mv^2_B\)となるので、
力学的エネルギー保存則より、
\(mgl\)=\(\Large\frac{1}{2}\)\(mv^2_B\)
\(v_B\)=\(\sqrt{2gl}\)となります。
(2) 小球が点Bを通過した後、糸は釘に引っ掛かりますので、糸全体の長さのうち、小球から距離\(r\)までの部分が、引き続き運動することになります。
よって、小球は点Cを中心とした半径\(r\)の円運動をします。
ここで、点Dも含めた図を以下に示します。
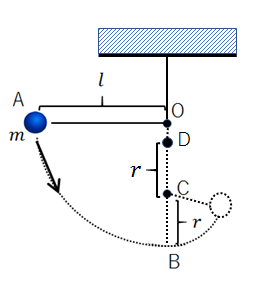
点Dは円運動をしている小球が到達する最高点ですが、小球にはたらく力は重力と張力のみなので、(1)と同様に力学的エネルギーは保存されています。
(1)と同じく最下点Bを位置エネルギーの基準とし、点Dにおける速度を\(v_D\)すると、点Dの力学的エネルギーは\(2mgr\)+\(\Large\frac{1}{2}\)\(mv^2_D\)となるので、点Aと点Dについて力学的エネルギー保存則を適用すると、
\(mgl\)=\(2mgr\)+\(\Large\frac{1}{2}\)\(mv^2_D\)
\(\Large\frac{1}{2}\)\(mv^2_D\)=\(mg(l-2r)\)
\(v_D\)=\(\sqrt{2g(l-2r)}\)
となります。
(3) 「糸がたるむ」というのは、張力が発生しなくなるということです。
まずは点Dにおける、糸の張力\(T_D\)を求めてみましょう。
小球が点Dに達した瞬間は、小球には張力以外に重力\(mg\)がはたらいています。
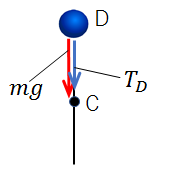
これらの力はともに円の中心方向で、合力は\(mg+T_D\)・・・・・①
です。
また、一般的に円運動をする物体には、中心方向に加速度が生じています。
(この加速度のおかげで、物体は円運動ができます。)
ある物体が速度\(v\)で半径\(r\)の円運動をしている時、物体に生じる加速度の大きさは\(\Large\frac{v^2}{r}\)と表されるので、点Dに達した際に物体に生じる加速度は、
\(\Large\frac{v^2_D}{r}\)・・・・・②
となります。
よって、運動方程式\(ma\)=\(F\)に①、②をあてはめると、
\(\Large\frac{mv^2_D}{r}\)=\(mg+T_D\)
を立てることができ、
(2)の結果も代入して\(T_D\)を求めると、
\(T_D\)=\(\Large\frac{mg(2l-5r)}{r}\)・・・・・③
となります。
ここで、小球が点Dに達した瞬間を考えますと、この時\(T_D\)=0であれば、小球はぎりぎり点Dを通過できます。
(点Dに達した時、\(T_D\)<0だと通過できません。)
よって、\(T_D\)=0の時の\(r\)が、小球が点Dを通過できる最大の半径(=\(r_m\))です。
③において\(T_D\)=0とすると、
\(\Large\frac{mg(2l-5r_m)}{r_m}\)=0
\(mg(2l-5r_m)\)=0
\(mg\)>0なので、\(2l-5r_m\)=0
∴ \(r_m\)=\(\Large\frac{2}{5}\)\(l\)
したがって、釘を打つ際に点Bからの位置を考える場合、糸全体の5分の2までであれば、小球は点Dを通過することがわかります。