図のように長さ\(l\)[m]、質量1.0[kg]の一様な棒ABを、水平であらい床と60°の角をなすように、鉛直でなめらかな壁に立てかけて静止させた。
このとき、棒の下端Aが床から受ける摩擦力の大きさと、垂直抗力の大きさを求めよ。
ただし、重力加速度を9.8\([m/s^2]\)とする。

「一様な棒」とありますので、棒には大きさがあるとみなします。
一般的に、大きさと質量がある物体を「剛体」といい、剛体における力のつり合いの条件は、以下のように二つあります。
●はたらく力の合力がゼロ
●力のモーメントの総和がゼロ
問題文のように棒が倒れずに静止しているのは、この二つの条件を満たしているからです。
まずは、棒の質量を\(m\)、重力加速度を\(g\)とおいて、棒にはたらく力を図示してみましょう。
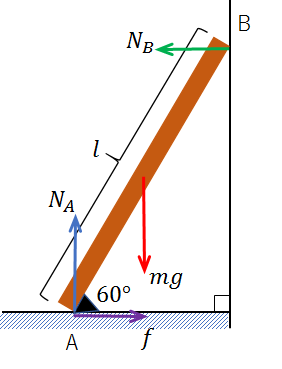
\(mg\)・・・棒にはたらく重力
\(f\)・・・棒が床から受ける摩擦力
\(N_A\)・・・棒が床から受ける垂直抗力
\(N_B\)・・・棒が壁から受ける垂直抗力
摩擦力\(f\)は水平右向きにはたらいており、棒が左側にすべり出すのを食い止めています。
書き出した力より、水平方向の力のつり合い式は、
\(f\)-\(N_B\)=\(0\)・・・・・①
鉛直方向の力のつり合い式は、
\(mg\)-\(N_A\)=\(0\)・・・・・②
となります。
次に力のモーメントですが、これはある支点の回りに回転させる力を指し、(力の大きさ)×(力の作用点から支点までの距離)で求められます。
今回は、点Aを支点として、棒にはたらく力のモーメントを求めてみます。
※「作用点から支点までの距離」は、力の向きに対して垂直方向であることに注意してください。
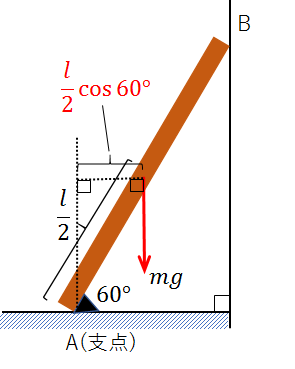
すなわち、重力\(mg\)の作用点から支点までの距離は\(\Large\frac{l}{2}\)\(cos60°\)、
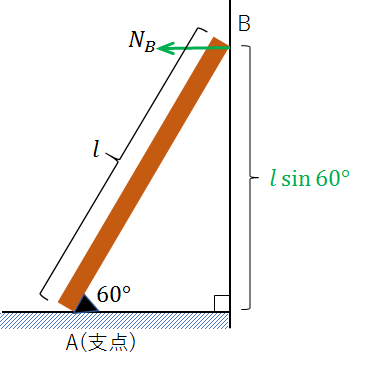
垂直抗力\(N_B\)の作用点から支点までの距離は\(lsin60°\)となります。
なお、点Aは支点そのものなので、点Aにはたらく力のモーメントは考えません。
以上より、時計回りを正とすると、力のモーメントのつり合い式は、
\(mg\)×\(\Large\frac{l}{2}\)\(cos60°\)-\(N_B\)×\(lsin60°\)=\(0\)・・・③
となります。
後は、これらをひとつひとつ解いていけば答えにたどり着きます。
まず②式より、\(N_A\)=\(mg\)=\(1.0×9.8\)=\(9.8[N]\)
また、③式より\(9.8\)×\(\Large\frac{l}{2}\)×\(\Large\frac{1}{2}\)-\(N_B×l\)×\(\Large\frac{\sqrt{3}}{2}\)=\(0\)
\(9.8\)×\(\Large\frac{1}{4}\)-\(N_B\)×\(\Large\frac{\sqrt{3}}{2}\)=\(0\)
\(\Large\frac{\sqrt{3}}{2}\)\(N_B\)=\(2.45\)
\(N_B\)=\(\Large\frac{2}{\sqrt{3}}\)×\(2.45\)≒\(\Large\frac{2}{1.73}\)×\(2.45\)≒\(2.82[N]\)
よって、①式より、
\(f\)=\(N_B\)≒\(2.82[N]\)
となります。