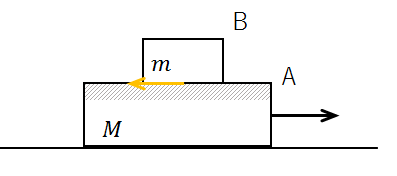
図のように、水平でなめらかな床面の上に質量\(M\)の物体Aを置き、さらにその上に質量\(m\)の物体Bを置いた。
この状態で、物体Aに水平方向右向きの力を加えたところ、物体AとBはそれぞれ別々に運動した。

物体AとBの間の動摩擦係数を\(μ'\)、重力加速度を\(g\)として、次の問いに答えよ。
(1) 物体Bにはたらく摩擦力の向きを求めよ。
(2) 物体Bの加速度の大きさを求めよ。
物体をのせた物体を引くと?で紹介したもののうち、「物体AとBが別々に運動する(一体となっていない)」バージョンです。
その中でも特に、物体Bの動きを分析していきます。
(1) 物体Bにはたらく摩擦力とのことですが、問題文より、物体Bは動いている状態なので、動摩擦力がはたらいています(「動摩擦係数をμ'として」とあるので、なんとなく予想できたかもしれませんが(笑))。
ここで一度物体Aに着目してみますと、物体Aは右向きに力が加わるので、右向きに動きます。
物体AとBの間には摩擦がはたらいていますので、物体Aも、動けば動摩擦力を受けることになりますよね。
動摩擦力は運動方向と逆向きにはたらくので、物体Aにはたらく動摩擦力は、水平方向左向きです。
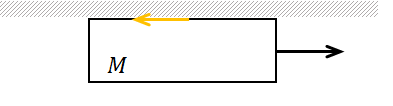
したがって、物体Bが受ける摩擦力はその逆なので、水平方向右向きとなります。
--------------------------------
(2) (1)の結果も踏まえて、物体Bにはたらく力を図示すると下記のようになります。
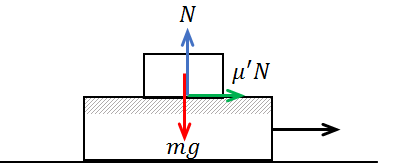
(※混乱を避けるため、物体Aにはたらく動摩擦力は消してあります。)
物体Bは運動しているので、まずは運動方程式を立ててみましょう。
物体Bにはたらく力は動摩擦力\(μ'N\)のみなので、運動方程式は、
\(ma\)=\(μ'N\)・・・・・①
また、物体Bは鉛直方向には動きませんから、鉛直方向にはたらく力はつり合っています。
よって、力のつり合い式より、
\(N\)=\(mg\)・・・・・②
②を①に代入すると、
\(ma\)=\(μ'mg\)
∴ \(a\)=\(μ'g\)
この結果より、物体Bの加速度は、物体Bの質量とは無関係であることがわかります。
物体Bの運動方向は?
物体をのせた物体を引くと?では物体Bが移動する方向についても書いていますが、ここでは身近な例を交えてお話します。
例えば、止まっているバスが急発進した状況を思い浮かべてみてください。
経験があるかもしれませんが、バスの中で立っている乗客は、発車した瞬間に後方に引っ張られますよね。
これは、バスが動き出したにもかかわらず、乗客は静止し続けようとしていたことで発生する状況です(「慣性の法則」といいます)。
これと同様に、今回、物体Bが動くような大きい力で物体Aを引っ張ると、物体Bはその場に静止し続けようとするので、物体Aから見て逆向き(左向き)に動こうとします・・・が!
今回、物体AとBの間には摩擦があるため、左向きに動こうとする物体Bには右向きの動摩擦力がはたらきます。
よって、結果的に右向きに力が加わった状態となるので、物体Bは右向きに動くのです。
ややこしいですが、物体にはたらく力をひとつひとつ考えていくことで運動の状態が見えてきますので、惑わされないようにしてください。