自由落下をする身近なものの一つに「雨粒」があります。
普段あまり意識しませんが、雨粒の速さは、自由落下の式を使って求めることができます。
----------------------------------
一般的に、雨雲の高さは500~2000[m]程度なので、仮に1000[m]の高さから雨粒が落ちてくるとしましょう。
地面に達する瞬間の雨粒の速さは、自由落下の時間を含まない式(\(v^2\)=\(2gy\))に\(g\)=9.8、\(y\)=1000を代入すると、
\(v^2\)=\(2×9.8×1000=19600\)
\(v\)=\(140[m/s]\)
時速になおすと504[km/h]です。新幹線よりも速いですね!
ですが普段雨を見た時に、こんな超絶なスピードで降り注いでいるように見えるでしょうか??もっとゆっくりな気もします。
実はこの雨粒の速さ、実際は時速30[km]程度だそうです。
なぜ高い場所から落ちてきているのに、ここまで遅くなるのでしょう?
実際には「空気抵抗」を受ける
地球上には、どこに行っても空気が存在します。
雨粒は、落下し始めてから地面に到達するまで空気中を移動するので、絶えずその抵抗を受け、速さが小さくなっていくのです。
この空気抵抗ですが、高校物理では速さに比例すると考えます。
ゆえに、雨粒が落下する速さを\(v\)とすると、空気抵抗は\(kv\)(\(k\)は比例定数)と表すことができます。
そしてもう一つ大切なのが、空気抵抗は、運動する向きと逆向きにはたらきます(摩擦力もそうでしたね)。
つまり、雨粒が重力の影響を受けて鉛直下向きに落下している時、空気抵抗は鉛直上向きにはたらいているということです。
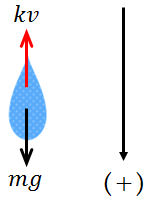
以上より、鉛直下向きを正とし、雨粒の質量を\(m\)、加速度を\(a\)とすると、雨粒の運動方程式は下記のようになります。
\(\large ma\)=\(\large mg-kv\)・・・・・①
----------------------------------
自由落下の式\(v^2\)=\(2gy\)からもわかるように、落下中の雨粒の速さ\(v\)は、落下距離に伴ってどんどん増えていきます。
しかし、①式において\(m\)と\(g\)は一定なので、\(v\)が増えていくと\(a\)は減っていきます。
つまり、加速する度合いがどんどん小さくなっていくというわけです。
やがて、\(kv\)が\(mg\)と等しくなると\(ma\)=0、すなわち\(a\)=0となって、加速しなくなります。
すなわち雨粒は等速直線運動をしていることになり、この時の速さが時速30[km]程度ということです。
雨雲から地面に到達するまでの雨粒の様子が、何となくイメージできましたでしょうか?