床からの高さが\(h\)のなめらかな台の上に、ばね定数\(k\)のばねが一端を固定して置かれており、ばねの片端には質量\(m\)の小球がつながれている。
このばねを、図のように自然長から\(x\)だけ縮めて静かに離したところ、ばねが自然長に戻ったと同時に小球がばねから外れ、小球はそのまま床の上に落下した。

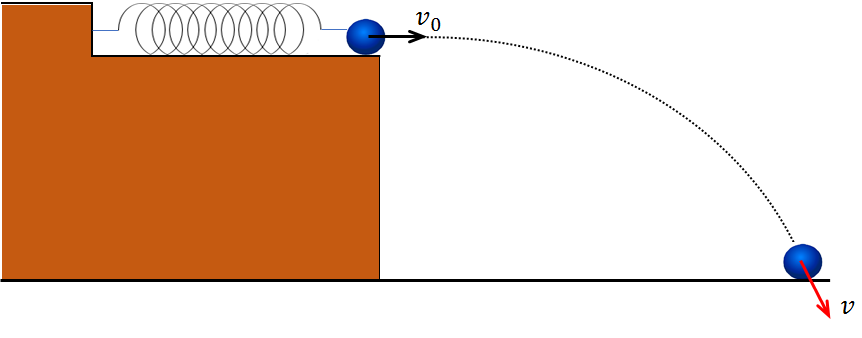
ばねが自然長に戻った時の小球の速さ\(v_0\)と、床に落下した瞬間の小球の速さ\(v\)を求めよ。
なお、ばねの自然長の位置は、台の右端とする。
ばねが元に戻る勢いによって、先端に取り付けた物体が投射される状況です。
このような場合、
●小球がばねに付いている状態
●小球がばねから離れた状態
の二通りに分けると、考えやすくなります。
小球がばねに付いている状態
これは、手を離してからばねが自然長に戻るまでの間です。
この間小球が受ける力は、重力とばねの弾性力、そして垂直抗力ですが、重力と弾性力は保存力であり、垂直抗力は小球の運動方向に対して垂直なので、小球に対して仕事をしません。
よって、手を離してからばねが自然長に戻るまでの間、力学的エネルギーは保存されています。
ばねが自然長の位置を基準とし、ばねが自然長に戻った瞬間の小球の速さを\(v_0\)とすると、
手を離すまではばねが自然長から\(x\)だけ縮んでいるので、力学的エネルギーはばねの弾性エネルギー\(\Large\frac{1}{2}\)\(kx^2\)のみです。
一方、ばねが自然長の状態では、ばねは基準から伸びても縮んでもいないので弾性エネルギーはゼロ、
その代わり速さ\(v_0\)で運動しているので、運動エネルギー\(\Large\frac{1}{2}\)\(mv^2_0\)をもっています。
よって、自然長の状態の力学的エネルギーは、運動エネルギー\(\Large\frac{1}{2}\)\(mv^2_0\)のみとなります。
したがって、力学的エネルギー保存則より、
\(\Large\frac{1}{2}\)\(kx^2\)=\(\Large\frac{1}{2}\)\(mv^2_0\)
\(v^2_0\)=\(\Large\frac{k}{m}\)\(x^2\)
∴ \(v_0\)=\(x\Large\sqrt{\frac{k}{m}}\)
と求めることができます。
小球がばねから離れた状態
小球がばねから離れてから床に落下するまでの間、小球にはたらいている力は重力のみなので、力学的エネルギーは保存されています。
床の高さを位置エネルギーの基準とすると、床に落下した瞬間の小球は運動エネルギー\(\Large\frac{1}{2}\)\(mv^2\)しかもってないので、これが床の地点における力学的エネルギーになります。
また、ばねから離れた瞬間の小球は、基準から高さ\(h\)の地点にあり、速さ\(v_0\)で運動していますので、位置エネルギー\(mgh\)と、運動エネルギー\(\Large\frac{1}{2}\)\(mv^2_0\)をもっています。
よって、力学的エネルギー保存則より、
\(\Large\frac{1}{2}\)\(mv^2\)=\(mgh\)+\(\Large\frac{1}{2}\)\(mv^2_0\)
\(v^2\)=\(2gh+v^2_0\)
∴ \(v\)=\(\sqrt{2gh+v^2_0}\)
と求めることができます。
水平投射として考えた場合
ばねから離れた後の小球の運動は、水平投射です。
水平投射では、物体の運動は水平向きと鉛直下向きに分解することができ、水平向きは等速直線運動、鉛直下向きは自由落下をしています。
今回、地上から\(h\)の高さより水平投射を行ったことになるので、自由落下の「時間を含まない式」を用いると、\(h\)だけ落下した後の速度の鉛直成分\(v_y\)は、
\(v_y\)=\(\sqrt{2gh}\)
となります。
なお、速度の水平成分は、投射時と変わらず\(v_0\)です(等速直線運動なので)。
よって、求める速さ\(v\)はこの二つの成分を合成したものなので、
\(v\)=\(\sqrt{2gh+v^2_0}\)
と求めることができます。