ばねをある程度まで引き伸ばした時、そのばねに取り付けられた物体は、手を離すと勢い良く戻ります。
戻る際に別の物体にぶつかれば、それをはね飛ばしたりします。
つまり、引き伸ばされたばねはそれだけでエネルギーをもっていることになり、このエネルギーを、「弾性力による位置エネルギー」、あるいは単に「弾性エネルギー」と言います。
<弾性力による位置エネルギー>
$$U=\frac{1}{2}kx^2$$
(\(U[J]\):弾性力による位置エネルギー、\(k\):ばね定数、\(x[m]\):自然長からの変位)
上式において、変位\(x\)は二乗されています。
つまり、\(x\)がプラスでもマイナスでも(ばねが基準点から\(x\)だけ伸びている場合も縮んでいる場合も)、ばねがもっている位置エネルギーは同じということです。

\(\frac{1}{2}\)がつく理由は?
弾性力による位置エネルギーの式において、\(kx^2\)の前に\(\frac{1}{2}\)がついているのはなぜでしょう?
これを解明するために、あるばねを、自然長から\(x\)だけ伸ばす状況を考えます。
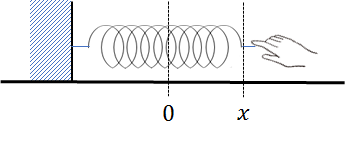
伸ばす際に手がばねに加える力は、フックの法則より\(kx\)です。
この力を加えたまま\(x\)だけ伸ばすので、仕事の定義式より、手がばねにした仕事は、\(kx\)×\(x\)
・・・と言いたいところですが、縦軸に加えた力、横軸に変位をとってこの状況をグラフに表すと、下記のようになります。

ばねには、伸ばせば伸ばすほど元に戻ろうとする力が強くなるといった特徴があります。
このため、ばねが伸びるにつれて、ばねを持つ手が加える力も徐々に大きくなっていきます。
ばねを伸び縮みさせる場合、加える力は一定ではないのです。

よって、手がばねにした仕事はグラフの三角形の面積部分なので、\(kx\)×\(x\)×\(\frac{1}{2}\)=\(\frac{1}{2}kx^2\)となります。
そして、手がばねに仕事をしたということは、言い換えれば、ばねは手から仕事をされています。
仕事をされたことで、ばねは他の物体に仕事をするためのエネルギーを蓄えたと考えると、弾性力による位置エネルギーも\(\frac{1}{2}kx^2\)であることがわかります。
--------------------
重力による位置エネルギーと同様に、弾性力による位置エネルギーも力学的エネルギーのひとつです。
形は似ていますが、運動エネルギー\(\frac{1}{2}mv^2\)とは全くの別物なので注意してください。
つまり、ばねの力学的エネルギーは、「弾性力による位置エネルギー\(\frac{1}{2}kx^2\)+運動エネルギー\(\frac{1}{2}mv^2\)」となります。