私たちは、「仕事」と聞くと人の役に立つもの、お金を稼ぐものなどとイメージしますが、物理の世界の「仕事」は、これらとは全く違った意味を持っています。
<物理における「仕事」>
物体に一定の力\(F\)[N]を加え続けて、その力の向きに距離\(s\)[m]だけ動かしたとき、力が物体にした仕事\(W\)[J]は、
\(W=F×s\)
である。

例えば、摩擦の無い水平面において、ある物体を60[N]の一定の力で水平に移動させる場合、結果的に物体が10[m]移動したとすれば、力が物体にした仕事は、60[N]×10[m]=600[J]です。
※もしも物体が力の向きに移動しなかった場合は、仕事をしたとは言えません。
(\(F\)[N]×0[m]=0[J])
例え莫大な力を加えたとしてもです。
どのくらい仕事をしたかは、加えた力と、その力の向きへの移動距離をセットで評価します。
----------------------------
さて、仕事の定義式を見ると、加えた力と移動距離との「掛け算」になっていますね。
つまり、縦軸に加えた力、横軸に移動距離をとったグラフを描くと、力が物体にした仕事は、その面積部分となるわけです。

なお、この式が成り立つためには、力は物体が移動し終わるまで継続して加え続ける必要があります。
上記の例では、物体が動き始めてから10[m]の地点で動き終わるまで、一貫して60[N]の力を加えないといけないということです。
また、もうひとつ大切なポイントとして、仕事の式が使える条件は、加えた力の向きと物体の移動した向きが同じ場合です。
もしも加えた力の向きと、物体が移動した向きが異なる場合は、互いに同じ向きになるよう考慮しなければいけません。
以下で説明していきます。
力の向きと移動する向きが異なる場合
下記のように、物体に対して斜めに力を加える状況を考えます。

このように引っ張って物体が水平方向に移動した場合、物体が動いた向きと加えた力の向きは違いますよね。
では、仕事は求められないのかというと決してそんなことはなく、下記のように加えた力を分解して、水平成分(青色)を使えばオーケーです。
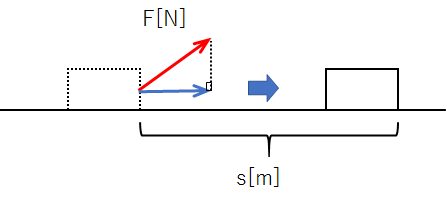
このようにすれば、物体が動いた向きと加えた力の向きは同じになります。
要は、物体の移動方向にはたらいている力(この場合は水平方向の力)さえ分かれば、仕事を求める式が適用できるわけです。
水平方向の力を求めるには、数学で習うベクトルと三角比を使います。
下記のように水平方向と力\(F\)とのなす角を\(θ\)とすると、加えた力の水平成分は\(Fcosθ\)となります。
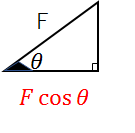
(あくまで物体を引っ張るための力は斜め方向に加えています。仕事の式を使うために、この力が水平方向にどのくらいはたらいているかを、考えるということです。)
以上のことから、仕事を求める式は下記の形でも表すことができます。
\(W=Fcosθ×s\)
(\(θ\)は、力\(F\)と物体の移動方向とがなす角)
もちろんこの式は、加えた力の向きと物体が移動する向きが同じ場合も使えます(同じ場合は\(θ\)が0°なので、\(cosθ\)=1となるから)
----------------------------
加える力の向きと物体が移動する向きが異なる場合の仕事の求め方は、イメージできましたでしょうか?
今後も仕事を求める際は、加えた力のうち物体の移動の向きにはたらいている力を、意識して考えるようにしてください。