「向心力」と「遠心力」は似ているようで全くの別物で、混乱しやすい概念のひとつです。
今回は、この向心力と遠心力の違いについて、考えていきましょう。
見ている人の立ち位置による
例えば、ある物体が点Oを中心として、一定の速さで水平向きに円運動しているとします。

そしてこの運動の様子を、AさんとBさんがそれぞれ見ているとしましょう。
向心力と遠心力を考える上で大切なのは、この二人が物体をどこから見ているかということです。
地上に立つAさん
Aさんは、動かない地上にじっと立って、物体の運動を眺めています。
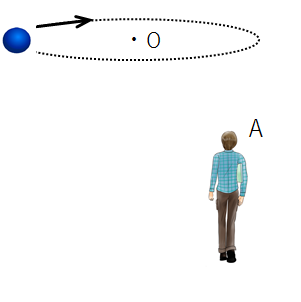
Aさんには、物体がまさに円運動をしているように見えるわけです。
ここで一旦、円運動そのものの話をしますと、一般的に等速円運動をする物体には、図のように中心方向に加速度が生じています。
(逆に言えば、この加速度が生じることで、物体は等速円運動をします。)

運動方程式より、加速度の向きとはたらく力の向きは同じですから、物体にはたらいている力も円の中心方向です。
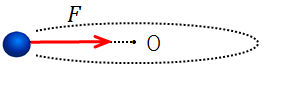
この力\(F\)が、まさに向心力です。
地上のAさんは、「物体は中心向きにはたらく力(=向心力)によって円運動をしているぞ」と思うわけです。
物体に乗っているBさん
一方Bさんは、Aさんと同じように物体を見ていますが、Bさん自らこの物体に乗って、物体と円運動しているとします。
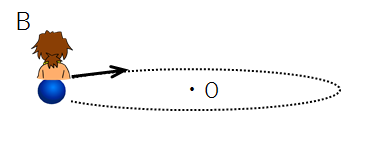
つまり、Bさんは物体と全く同じ動きをしているので、Bさんから物体は静止しているように見えます。
ここで、Bさん自身にはたらく力を考えてみましょう。
先程と同じように、物体には中心方向に力(=向心力)がはたらいています。
であるとすれば、物体に乗っているBさんも円の中心方向に絶えず引っ張られるはずですが、実際はそのまま動くことなく乗り続けられます。
これは、「Bさんは向心力以外の力も受けているから」
もっと言うと、
「向心力と真逆の向きに、向心力と同じ大きさの力がはたらいているから」
と解釈できます。
このような、向心力と真逆の向きにはたらく力を「遠心力」といいます。
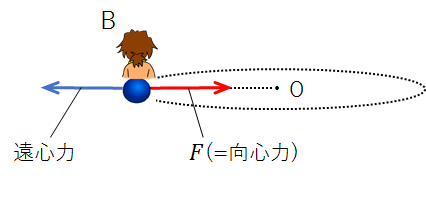
この二つの力のバランスが取れているおかげで、Bさんは円の中心方向に引っ張られたり、逆に中心と真逆の向きに投げ出されたりすることはありません。
遊園地でお馴染みのメリーゴーランドも、このように向心力と同じ向きに遠心力がはたらいているので、私たちはそのまま馬に乗っていられるのです。
--------------------------
遠心力は、観測者が円運動している物体に乗っている場合、その観測者のみにはたらく力です。
なので厳密には、円運動を地上で見ている人が「遠心力」という言葉を使うのは不適切とされています。
地上で見ている人は、円運動をしている物体には遠心力がはたらいていると「みなして」、つまり「仮の力」として扱います。
ややこしいですよね(笑)。
<向心力>
⇒円運動をする物体にはたらく、中心方向の力
<遠心力>
⇒回転座標系にはたらく、向心力と大きさが同じ逆向きの力
「回転座標系」とは、Bさんと物体のように回転しているものの総称、あるいはそのように定義する世界で、大学の物理学で詳しく扱います。
本当にざっくり言えば、AさんとBさんとでは物理的に置かれている状況が違うので、はたらく力の関係性も明確に区別しよう、ということです。
問題ではどのように使う?
実際の問題では、「観測者が地上で見ている」とか「観測者が物体と共に円運動している」といった記述は無いことが多いです。
では、式を立てる際に遠心力を使えないのかというと、そんなことはありません。
ただし使う場合は、その使い方に注意しなければなりません。
遠心力を使って式を立てる場合、力のつり合い式として立てる
なぜかと言いますと、遠心力は、向心力とつり合う見かけの力だからです。
なので「運動方程式」には使えません。
逆に運動方程式として使えるのは、「向心力」です。
繰り返しになりますが、遠心力は、回転している物体に乗っている観測者にはたらく仮の力ということを、覚えておいてください。