図のように、小球が速度\(v_o\)で滑らかな床に衝突して跳ね返った。
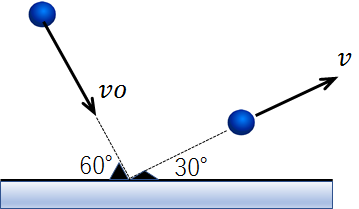
(1)跳ね返った後の小球の速度\(v\)を求めよ。
(2)小球と床との間の反発係数\(e\)を求めよ。
問題文には「滑らかな床」とありますので、小球と床との間に摩擦は発生しません。
そして跳ね返るということは、反発係数の式を使えそうなことが何となく予測できます。
(反発係数の式は、物体が別の物体に対して真っ直ぐ水平に衝突する際に適用できました。)
しかし、今回の衝突の方向は斜めです。
まずは斜めであることを、一旦意識から外してしまいましょう。
------------------------------
速度は大きさと向きをもっているため、ベクトルを使って分解できます。
これにしたがって、衝突前と衝突後の速度を水平成分と鉛直成分に分けると、下記の図のようになります。
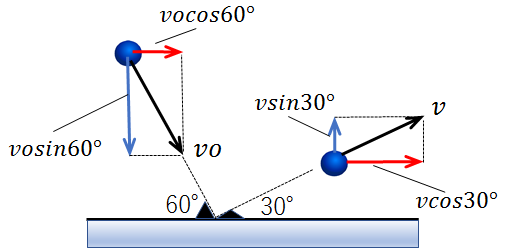
そして重要なのが、速度を分解したら、元の斜めのベクトルについては一旦無視します。
小球の実際の運動方向は確かに斜めですが、速度を水平成分と鉛直成分に分解した時点で、考えるのはあくまで水平成分と鉛直成分のみです。
床にぶつかることで、水平成分に働く力と、鉛直成分に働く力がどうなるかだけ、見ていきましょう。
水平成分
上の図から速度の水平成分だけ抜き出したものが、下記の図です。
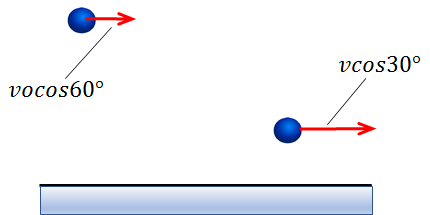
見てのとおり、床に対して常に水平です。
もしもザラザラした床だったり(=摩擦があったり)、衝突する瞬間に思い切り水平向きに力が加われれば、水平成分の速度も影響を受けますが、今回、そのようなことはありません。
つまり速度の水平成分は、衝突前と衝突後で変わりません。
よって、\(v_ocos60°\)=\(vcos30°\)
\(\Large\frac{v_o}{2}\)=\(\Large\frac{\sqrt{3}v}{2}\)
\(v\)=\(\Large\frac{v_o}{\sqrt{3}}\)
となります。
鉛直成分
逆に速度の鉛直成分だけ抜き出したものが、下記の図です。
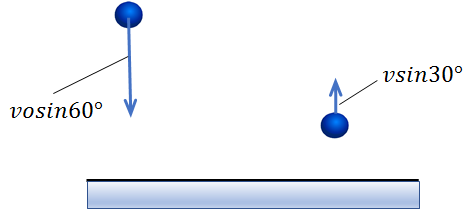
衝突前は床に対して鉛直下向き、衝突後は鉛直上向きであることが分かります。
これは、物体の衝突と反発係数でも紹介しました、物体が壁にぶつかって跳ね返る状況と全く同じです。
ここで鉛直下向きを正とすると、衝突後の速度は向きが逆なのでマイナスがつきます。
跳ね返り係数の式(\(e\)=\(-\Large\frac{v}{v_o}\))に当てはめると、
\(e\)=\(-\Large\frac{-vsin30°}{v_osin60°}\)
=\(\Large\frac{v}{2}\)*\(\Large\frac{2}{\sqrt{3}v_o}\)
=\(\Large\frac{v}{\sqrt{3}v_o}\)・・・①
(1)より\(v\)=\(\Large\frac{v_o}{\sqrt{3}}\)であるから、これを①に代入すると、
\(e\)=\(\Large\frac{1}{3}\)
となります。
分解して別々に考える
結局、衝突後の速度は水平成分から、反発係数は速度の鉛直成分から、それぞれ求めることができました。
このように衝突の方向が斜めの場合は、分解して別々に考えることで解きやすくなります。
今後も頻繁に使う方法ですので、頭の中に入れておいてください。