密度が900[kg/\(m^3\)]の氷山があり、その一部が海面上に出ている。
出ている部分の体積は、氷山全体のおよそ何%か。
ただし、海水の密度は1020[kg/\(m^3\)]とする。
氷山とは、莫大な大きさの氷河の一部が海に落ち、浮かんでいるものです。
「山」とあるので、海底から積み上がったものと誤解しやすいですが、浮かんでいることに注意してください。
図で表すと下のようになります。

このうち、海面上に出ている部分、すなわち斜線部分の体積は氷山全体の何パーセントか?というのが今回の問題です。
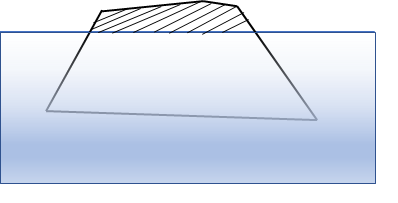
---------------------------------
あらためて状況を見ますと、氷山は、一部を海面上に出した状態で浮かんでいる、すなわち静止しています。
この「静止している」というのがとても大切なポイントです。
なぜなら、一般的に物体が静止するのは、その物体にはたらく力がつりあっているからです。
では今回、氷山にはたらく力は何でしょうか?
まずは、氷山全体にはたらく重力です。
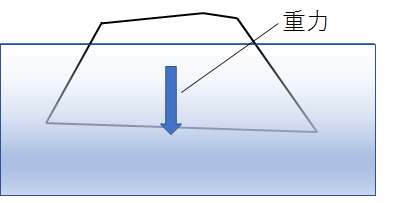
どこでどのような状況にいようとも、この地球上に存在するもの全てが、重力の影響を受けるのでした。
氷山の密度は900[kg/\(m^3\)]なので、1[\(m^3\)]の質量は900[kg]です。
よって、重力加速度を\(g\)とすると、1[\(m^3\)]の氷山にはたらく重力は、900×\(g\)となります。
なお、受ける重力の向きは「鉛直下向き」です。
そして、氷山は海の中にあるので、浮き上がらせようとする力、すなわち浮力も受けています。
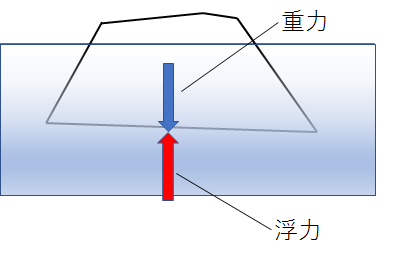
アルキメデスの原理ってどんなもの?より、「流体中の物体は、その物体が押しのけている流体の重さと同じ大きさの浮力を受ける」ので、
まずは氷山が押しのけている海水の重さを求めなければなりません。
海水を押しのけているのは、氷山全体のうち海水に浸かっている部分なので、この部分の体積を\(V[m^3]\)としましょう。
海水の密度は1020[kg/\(m^3\)]なので、押しのけている海水の質量は、1020×\(V\)です。
よって、押しのけられた海水の重さは、重力加速度\(g\)を用いて「1020\(×V×g\)」となります。
ちなみに浮力は、「鉛直上向き」にはたらきます。
この二つの力のつりあい式を立てると、
900\(×g\)=1020\(×V×g\)
\(V\)=\(\frac{900}{1020}\)≒0.882
よって、海水に浸かっている部分は、氷山全体のおよそ88.2パーセントになります。
今回求めたいのは海面上に出ている部分なので、
100-88.2=11.8[%]
が答えとなります。