自由落下と鉛直投射では、物体の運動は一直線上に限られていましたが、今回お話する「水平投射」では、物体は平面上を運動します。
運動の経路は2次元ですが、紐解いていくと、自由落下や鉛直投射が元になっていることがわかります。
まずは経路を分解せよ
水平投射とは、名前のとおり水平向きに初速度を与えて、物体を勢いよく投げ出す運動です。
投げ出された物体は、初めは初速度の向きに進みますが、重力にまかせて徐々に下向きに落下していきます。

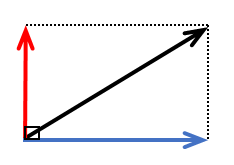
ここで、上の図に対して、水平向きにx軸、鉛直向きにy軸を定めてみましょう。

実際は斜め方向に運動している物体ですが、x軸方向とy軸方向単独で見てみますと、それぞれ図のような動きをしています。

ここで一旦基本に立ち返りますが、
そもそも、投げ出した物体はなぜ落ちていくのでしょうか?
それは、鉛直下向きに重力が働いているからです。落下中の物体は重力の影響をまず、受けているんですね。
ではなぜ、真下に落ちずに斜め下に落ちていくのでしょうか?
それは、初めに水平方向に勢い(=初速度)を与えたからです。落下中の物体は重力に加えて、初速度の影響も受けているんですね。
●水平に勢い良く投げ出された物体
水平方向
⇒初速度の影響を受ける
鉛直方向
⇒重力の影響を受ける
例えば自由落下のように、何もせずにただ物体をそっと離せば、そのまま真下に落ちていきます。
ですが今回は、初めに水平方向に初速度を与えたことで、水平方向にはその初速度の影響を、鉛直方向には重力の影響をそれぞれ受けているのです。
このため物体は、これら水平方向と鉛直方向の
各成分を合成した「斜め下方」に、実際に落ちていってるわけです。
-------------------------
物体の経路が各成分の合成で成り立っているので、逆に言えば、物体の経路は好きなように分解できます。
この時に高頻度で使うのが、高校数学で習う「ベクトル」です。

ベクトルの分解の仕方はたくさんありますが、少なくとも高校物理では、x軸とy軸が直行した「直交座標」しか扱いませんので、水平成分と鉛直成分が直角になるように分ければオーケーです。
2次元の運動では、このように運動をいくつかの成分に分けることを、まず初めに行います。
こうすることで、一見複雑そうに見えても、単純な運動の組み合わせであることがわかるからです。
水平投射の各成分の運動
あらためて物理用語を使うと、水平投射において、物体の軌道の水平成分と鉛直成分はそれぞれ下記のような運動をします。
●水平投射の物体の運動
水平成分・・・等速直線運動をする
鉛直成分・・・自由落下をする
水平方向に初速度のまま進む理由としては、水平方向には、運動を妨げたり補助したりするものが何もないからです。
重力のみがはたらいている空間を運動している限り、地上などに落下するまで、ずっと初速度を保ったままです。
このことから、水平成分と鉛直成分の速度や変位を求める時は、等速直線運動と自由落下の公式が、それぞれ使えます。
つまり、仮に初速度を\(v_0\)とした場合、t秒後の物体の速度の水平成分\(v_x\)と変位\(x\)は、
\(v_x=v_0\)
\(x=v_0t\)
また、\(t\)秒後の物体の速度の鉛直成分\(v_y\)と変位\(y\)は、
\(v_y\)=\(gt\)(\(g\)は重力加速度)
\(y=\frac{1}{2}gt^2\)
となります。
(自由落下の式については、鉛直下向きを正としています。)
-------------------------
一見どこから手をつけてよいかわからないような斜め向きの運動でも、このように動きを分解することで、シンプルな運動の組み合わせとして考えることができます。