「水平投射」では、移動する物体の運動を、水平方向と鉛直方向に分けて考える方法をお話しました。
今回紹介する斜方投射も、考え方は同じです。
斜方投射も経路を分解
斜方投射とは名前のとおり、物体などを斜め向きに勢いよく投げるものです。
物体は、しばらくは投げ出された方向に進みますが、次第に向きを変え、斜め下方に落下していきます。

水平投射と同様に、運動を水平方向と鉛直方向に分け、個別に考えていきましょう。
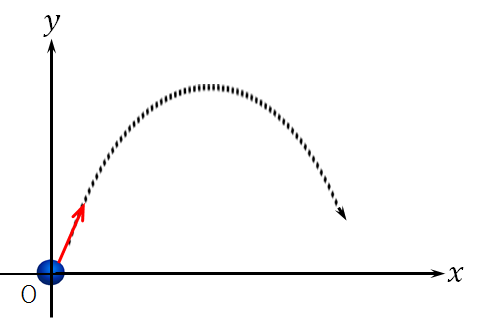
斜方投射では、水平方向と鉛直方向では、それぞれ下記のような運動をしています。
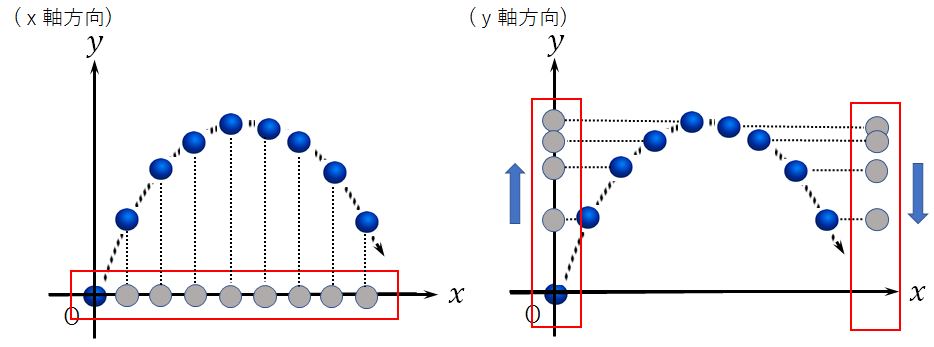
鉛直(y軸)方向では、物体は一旦上昇していますよね。
鉛直下向きに重力がはたらいているので、本来物体は真下に落ちていくはずですが、初めに勢い(=初速度)を与えたことで、重力と初速度の両方の影響を受けているからです。
水平方向についても、同じく初速度の影響を受けて等速で進んでいきます。
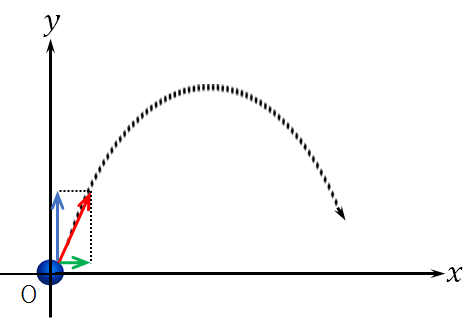
(パッと見、初速度は斜め向きですが、分解すると、水平向きにも鉛直上向きにも影響を及ぼしていることが分かります。)
このように、鉛直方向も初速度の影響を受ける点が、水平投射との大きな違いです。
●斜めに勢い良く投げ出された物体
水平方向
⇒初速度の影響を受ける
鉛直方向
⇒初速度と重力の影響を受ける
投げた瞬間は初速度の勢いがあるため、物体は斜め上方にどんどん進んでいきます。
しかし、鉛直方向はしばらく経つと上向きの初速度の勢いが無くなり(=最初の図の「山のてっぺん」)、その後は重力の影響を受けて下向きに運動し始めます。
水平方向の速度は初速度のままなので、物体は、水平方向と鉛直方向の成分を合成した「斜め下方」に、落ちていくわけです。
斜方投射の各成分の運動
水平投射と同じく物理用語を使うと、物体の軌道の水平成分と鉛直成分はそれぞれ下記のような運動をします。
●斜方投射の物体の運動
水平成分・・・等速直線運動をする
鉛直成分・・・鉛直上方投射をする
このことから、水平成分と鉛直成分の速度や変位を求める時は、等速直線運動と鉛直上方投射
の公式が、それぞれ使えます。
------------------------
斜方投射の特徴は、初速度が斜め向き、すなわち角度が付いていることです。
今回、物体を投射する位置を基準とし、水平方向から\(θ\)だけ傾けて、投射するとしましょう。
先程も少し分解の図を出しましたが、投射する瞬間から角度が付いているため、初速度も水平方向と鉛直方向に分解してあげないといけません。
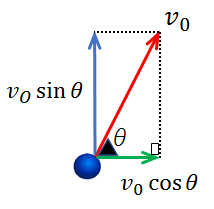
仮に初速度を\(v_0\)とした場合、初速度の水平成分は\(v_0cosθ\)、鉛直成分は\(v_0sinθ\)となります。
よって、物体の速度の水平成分\(v_x\)は、
\(v_x\)=\(v_0cosθ\)
\(t\)秒後の物体の変位\(x\)は、
\(x\)=\(v_0cosθ*t\)
となります。
また、\(t\)秒後の物体の速度の鉛直成分\(v_y\)は、鉛直上方投射の式から、
\(v_y\)=\(v_0sinθ\)-\(gt\)(\(g\)は重力加速度)
同じく\(t\)秒後の物体の変位\(y\)は、
\(y\)=\(v_0sinθ*t\)-\(\Large\frac{1}{2}\)\(gt^2\)
となります。
(鉛直上方投射の式では、鉛直上向きを正としています。)
なぜ速度の水平成分は変化しない?
念のための確認になりますが、水平投射も斜方投射も、水平成分の速度がずっと初速度のままなのはなぜでしょうか?
理由は、水平方向には運動を変化させる力がはたらかないためです。
(厳密には空気の抵抗を受けますが、高校物理では、空気抵抗は無視して考える場合がほとんどです。)
これが例えば、運動中に意図的に物体を手で押したりすれば、水平方向にも力が加わるので運動状態が変化します。
------------------------
なお、鉛直方向は「重力」という運動を変化させる力がはたらいているので、物体の速度が大きくなったり小さくなったりします。
ちなみに、このような運動の最中以外でも、この世に存在する限り重力の影響は受け続けます。
ですので問題文にも、わざわざ「重力を受けるものとする」とは書かれていません。
重力を受けている前提で「重力加速度は\(g\)とする」などと書かれていますので、そのつもりでいてください。