質量\(m\)の物体が、速度\(v_0\)の状態から距離\(L\)だけ移動し、速度が\(v_1\)に増加したとします。

この様子を等加速度運動の公式の中の「時間を含まない式」を使って表してみましょう。
時間を含まない式とは、次のようなものでした。
\(v^2-v^2_0\)=\(2ax\)
この式の\(v\)に\(v_1\)、\(v_0\)に\(v_0\)、\(x\)に\(L\)をそれぞれ代入すると、
\(v^2_1-v^2_0\)=\(2aL\)
両辺に\(\large\frac{m}{2}\)をかけると、
\(\large\frac{m}{2}\)\(v^2_1\)-\(\large\frac{m}{2}\)\(v^2_0\)=\(maL\)・・・・・①
また、物体の運動方程式は、加速度を\(a\)、加える力を\(F\)とすると\(ma\)=\(F\)と表されるので、これを①の右辺に代入すると、
\(\large\frac{m}{2}\)\(v^2_1\)-\(\large\frac{m}{2}\)\(v^2_0\)=\(FL\)・・・・・②
となります。
この式をちょっと見てみますと、\(\large\frac{m}{2}\)\(v^2_1\)は\(L\)だけ進んだ物体がもつ運動エネルギー、\(\large\frac{m}{2}\)\(v^2_0\)は進む前において物体がもつ運動エネルギーです。
つまり、②の左辺は運動エネルギーの変化量を表しています。
また、ある力がした仕事は、(力の大きさ)×(力の向きへの移動距離)なので、②の右辺は物体に加わった力がした仕事、すなわち物体がされた仕事を表しています。
したがって、物体の運動エネルギーの変化は、その物体にされた仕事に等しいことがわかります。
これを「エネルギーの原理」といいます。
※別項で紹介している「力学的エネルギーの差分=非保存力がした仕事」と似ています。
また、②を変形すると、
\(\large\frac{m}{2}\)\(v^2_0\)+\(FL\)=\(\large\frac{m}{2}\)\(v^2_1\)
となりますが、これは速度\(v_0\)の物体が\(L\)移動する間、ずっと力\(F\)を加え続け、結果的に速度が\(v_1\)になったものと解釈できます。
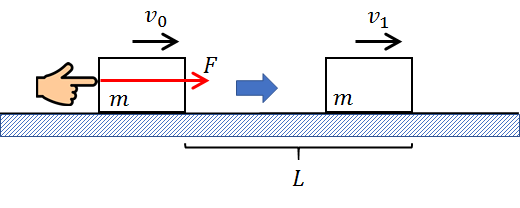
「右向きに動く物体に力を加えて補助したので、速度が増加した」というイメージです。
----------------------------
今度は、質量\(m\)の物体が、速度\(v_0\)の状態から距離\(L\)だけ移動し、速度が\(v_1\)に減少したとします。
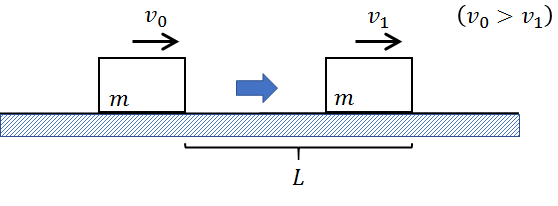
等加速度運動の式から①を導くところまでは同じですが、ポイントは運動方程式との照らし合わせです。
この場合は減速しているので、負の加速度がはたらいています。
よって、運動方程式は\(m(-a)\)=\(F\)となり、\(ma\)=\(-F\)なので、これを①に代入すると、
\(\large\frac{m}{2}\)\(v^2_1\)-\(\large\frac{m}{2}\)\(v^2_0\)=\(-FL\)・・・・・③
が導けます。
また、③を変形すると、
\(\large\frac{m}{2}\)\(v^2_0\)-\(FL\)=\(\large\frac{m}{2}\)\(v^2_1\)
となりますが、これは速度\(v_0\)の物体が\(L\)移動する間、ずっと移動方向と逆向きに力\(F\)を加え続け、結果的に速度が\(v_1\)になったものと解釈できます。
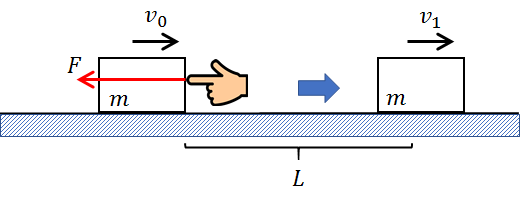
「右向きに動く物体に力を加えて進行を妨げたので、速度が減少した」というイメージです。