ロケットに物体が結合する問題

現実に起こる頻度は少ないですが、ロケットの一部が分裂する問題の逆パターンになります。

分裂する場合と同様、ロケットと燃料は、衝突する瞬間に互いに及ぼし合う力のみを受けるので、衝突前と衝突後とで運動量は一定です。

同じ要領で、運動量保存則の式を立ててみましょう。

＜衝突前＞

ロケットと燃料は、まだ別々に進んでいます。
よって、ロケットと燃料の質量はそれぞれ\(M\)、\(m\)、ロケットと燃料の速度はそれぞれ\(\overrightarrow{V_0}\)、\(\overrightarrow{v}\)です。

＜衝突後＞

衝突後は一体となっているので、質量は\(M\)＋\(m\)、速度は問題文のまま\(\overrightarrow{V}\)です。
(ちなみに燃料の速度も、一体となっているので\(\overrightarrow{V}\)です。)

-----------------------------

よって、運動量保存則の式は、

\(M\)\(\overrightarrow{V_0}\)＋\(m\)\(\overrightarrow{v}\)＝(\(M＋m\))\(\overrightarrow{V}\)

となり、この式から衝突後のロケットの速度は、

\(\overrightarrow{V}\)＝\(\Large\frac{M\overrightarrow{V_0}＋m\overrightarrow{v}}{M＋m}\)・・・・・①

と求めることができます。

速さを代入する時は符号に注意

最後に、求めた式に具体的な値を入れてみますが、特に速さが与えられた時は注意が必要です。

なぜなら、速さは速度と違って向きをもっていないので、場合によってはそのまま代入できないからです。

例として、次の二通りの衝突を考えてみます。

●燃料がロケットに追い付く形での衝突
●燃料とロケットが互いに向かい合った衝突

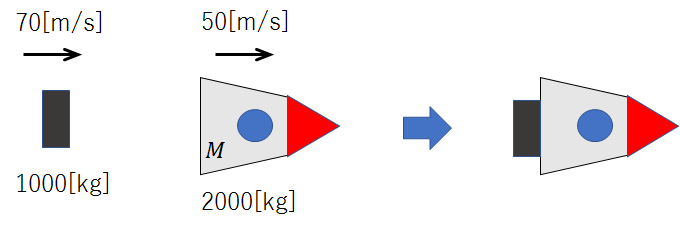
ロケットと燃料の進む向きは、どちらも右向きですね。

なので右向きを正とすると、速度もロケットと燃料それぞれ50[m/s]、70[m/s]となるので、値はそのまま代入できます。

\(\overrightarrow{V_0}\)＝50、\(M\)＝2000、\(\overrightarrow{v}\)＝70、\(m\)＝1000を①式に代入して、

\(\overrightarrow{V}\)＝\(\Large\frac{2000×50＋1000×70
}{2000＋1000}\)＝\(\Large\frac{170000}{3000}\)

≒\(56.7[m/s]\)

衝突後は、右向きにおよそ56.7[m/s]の速さで進むことがわかります。

この場合、ロケットと燃料の進む向きは、互いに逆向きですね。

なので右向きを正とすると、燃料は正の向きですが、ロケットは負の向きに進んでいることになります。

よって、燃料の速度は70[m/s]、ロケットの速度は－50[m/s]となります。

速度は速さと違って向きをもっており、正と決めた向きと逆向きに進んでいれば、マイナスがつくからです。

ゆえに、\(\overrightarrow{V_0}\)＝－50、\(M\)＝2000、\(\overrightarrow{v}\)＝70、\(m\)＝1000を①式に代入して、

\(\overrightarrow{V}\)＝\(\Large\frac{2000×(－50)＋1000×70
}{2000＋1000}\)＝\(\Large\frac{{－30000}}{3000}\)

≒\({－10}[m/s]\)

衝突後は、左向きに10[m/s]の速さで進むことがわかります。
(速度で表すと、「－10[m/s]で進む」となります。)

-----------------------------

念押しになりますが、

「大きさをもっているもの」が速さです。
「大きさと向きをもっているもの」が速度です。
(速さと速度の違い)

元々向きをもっている速度は、プラスやマイナスをつけるだけで向きを表すことができますが、速さはそれができません。(「マイナスの速さ」というのはありません。)

なので、速度の式に速さを代入する時は、運動の向きによって符号が変わることに注意してください。