運動量と力積でも示したとおり、質量と速度をかけたものを「運動量」といいます。
運動量保存則とは、この運動量に関係した法則です。
<運動量保存則>
物体系が内力を及ぼしあうだけで外力を受けていないとき、その物体系の運動量の総和は変わらない。
外力というのは、例えば手の力や、摩擦がある面などが該当します。
このような力が一切はたらかない場合に、運動量が保存されるということです。
物体系とは、ある物体とそれに関係する他の物体全てを、まとめて考えた時の呼び名です。

このことから、運動量保存則は二つ以上の物体について成り立つと言えます。
以下に、運動量保存則に関係した具体的な例を挙げてみます。
----------------------------
(例)質量\(m_A\)の物体A、質量\(m_B\)の物体Bがそれぞれ速度\(v_A\)、\(v_B\)で運動しているとし、これらが互いに衝突した後、それぞれ速度\(v'_A\)、\(v'_B\)になったとします。

衝突前のそれぞれの運動量は、
物体A・・・\(m_Av_A\)
物体B・・・\(m_Bv_B\)
よって、衝突前の運動量の総和は、
\(m_Av_A+m_Bv_B\)・・・①
また、衝突後のそれぞれの運動量は、
物体A・・・\(m_Av'_A\)
物体B・・・\(m_Bv'_B\)
よって、衝突後の運動量の総和は、
\(m_Av'_A+m_Bv'_B\)・・・②
この運動において、物体AとBに外力ははたらいていません。
衝突する瞬間については、物体Aは衝突によって物体Bに力を及ぼし、その反作用として自らも力を受けます。
物体Bも同様です。
この力は、物体AとBが互いに及ぼす力なので、外力ではありません。

このような力は、「内力」といいます。
したがって、運動量保存則が成り立つ条件を満たしているので、①=②となります。
\(m_Av_A+m_Bv_B\)=\(m_Av'_A+m_Bv'_B\)
重力は外力
既に気づいているかもしれませんが、運動している物体AとBには、常に重力がはたらいていますよね。
この重力、実は外力に相当します。
「外力がはたらくなら、運動量保存則は使えないのでは?」と思うかもしれません。
ですが、上記のような例では衝突時間が極めて短いため、重力が及ぼす影響も無視できるのです。
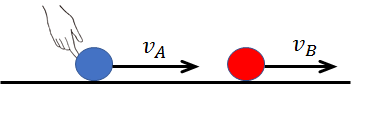
上図のように、衝突の瞬間や、その前後に意図的に力を加えた場合は、物体系は外力を受けたことになりますが、
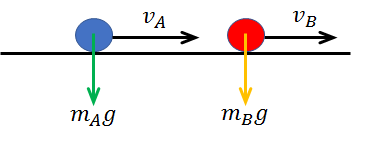
重力に関しては、はたらく向きが鉛直下向きで、横向きの運動や衝突にはほとんど関与しないため、影響を考えなくても良いということです。